▷ EJERCICIOS RESUELTOS DE ECUACIONES

¡Bienvenid@ a ejerciciosecuaciones.com!
En esta página web encontrarás ejercicios resueltos paso a paso de todo tipo de ecuaciones.
¡Esperamos que te guste la página web y que te sea útil!

Índice

Ejercicios de ecuaciones de primer grado

➤ Ver: cómo resolver ecuaciones de primer grado

Ejercicio 1

Resuelve la siguiente ecuación de primer grado:

$3x-2=x+4$

Ver solución

En primer lugar, pasamos los términos con x al miembro izquierdo de la ecuación y los números sin x al miembro derecho. Ten presente que al cambiar de miembro un término se debe cambiar su signo:

$3x-x=2+4$

Ahora agrupamos los términos de cada miembro de la ecuación de primer grado:

$2x=6$

Por último, despejamos la x pasando su coeficiente al otro lado dividiendo:

$x=\cfrac{6}{2}$

Y resolvemos la división resultante:

$x=3$

Ejercicio 2

Halla la x de la siguiente ecuación de primer grado:

$9x+5-2x=11-3x+4$

Ver solución

Primero colocamos los términos con x en el lado izquierdo de la ecuación y los términos sin x en el lado derecho. Recuerda que al cambiar un término de lado también se debe cambiar su signo:

$9x-2x+3x=-5+11+4$

En segundo lugar, hacemos las sumas algebraicas de los dos lados de la ecuación:

$10x=10$

Y, finalmente, despejamos la x de la ecuación de primer grado:

$x=\cfrac{10}{10}$

$x=1$

Ejercicio 3

Despeja la x de la siguiente ecuación de primer grado:

$7x+19=9x-6-2x$

Ver solución

El primer paso para resolver ecuaciones de primer grado es pasar todos los términos similares al mismo lado de la ecuación. Así pues, ponemos todos los términos con incógnita a la izquierda y todos los otros términos a la derecha:

$7x-9x+2x=-19-6$

Luego hacemos las sumas o restas de cada lado de la ecuación

$0x=-25$

$0=-25$

Sin embargo, en este caso la ecuación nunca se podrá cumplir, ya que 0 no es equivalente a -25. Es decir, independientemente del valor de la x, nunca se cumplirá la igualdad. Por lo tanto, es una ecuación de primer grado sin solución.

Para saber más acerca de las ecuaciones sin soluciones, puedes consultar el artículo enlazado más arriba.

Ejercicio 4

Calcula el valor de la x para que se cumpla la siguiente ecuación de primer grado:

$15x-8+27x+20=21-x+35+42$

Ver solución

El primer paso para determinar la solución de una ecuación de primer grado es pasar todos los términos con x a un lado y los otros términos al lado opuesto. Teniendo en cuenta que al cambiar de lado un término también se debe cambiar su signo, la ecuación queda:

$15x+27x+x=8-20+21+35+42$

Ahora agrupamos los términos de los dos miembros de la ecuación:

$43x=86$

Para terminar, despejamos la incógnita de la ecuación de primer grado:

$x=\cfrac{86}{43}$

$x=2$

Ejercicio 5

Encuentra la solución de la siguiente ecuación de primer grado:

$46+49x-15+21x+8x=92-39x+14+67x$

Ver solución

Primero pasamos los términos con incógnita al miembro izquierdo de la ecuación y los términos sin incógnita al otro miembro de la ecuación:

$49x+21x+8x+39x-67x=-46+15+92+14$

En segundo lugar, sumamos los términos de cada miembro de la ecuación:

$50x=75$

Despejamos la incógnita de la ecuación:

$x=\cfrac{75}{50}$

Y, finalmente, simplificamos la fracción al máximo:

$x=\cfrac{75}{50}=\cfrac{15}{10}=\cfrac{3}{2}$

Ejercicio 6

Resuelve la siguiente ecuación de primer grado con paréntesis:

$4x+6\left(x+3\right)=5x-2$

Ver solución

El primer paso es quitar el paréntesis de la ecuación. De modo que aplicamos la propiedad distributiva para solucionar el paréntesis:

$4x+6\cdot x+6 \cdot 3=5x-2$

$4x+6x+18=5x-2$

Ahora transponemos los términos para poner los que tienen x a la izquierda y los que no tienen x a la derecha:

$4x+6x-5x=-2-18$

Agrupamos los elementos que son semejantes:

$5x=-20$

Y, para terminar, despejamos la incógnita pasando el 5 dividiendo al otro lado de la ecuación:

$x=\cfrac{-20}{5}$

$\bm{x=-4}$

Ejercicio 7

Calcula la siguiente ecuación de primer grado con dos paréntesis:

$-4\left(-5x+1+7x\right)-2=x+\left(5-2x\right)\cdot 3$

Ver solución

Primero de todo debemos eliminar los paréntesis de la ecuación lineal. Por lo tanto, aplicamos la propiedad distributiva para calcular tanto el paréntesis de la izquierda como el de la derecha:

$-4\cdot (-5x)-4\cdot 1-4\cdot 7x-2=x+5\cdot 3-2x\cdot 3$

$20x-4-28x-2=x+15-6x$

Hacemos la transposición de los términos:

$20x-28x-x+6x=15+4+2$

Agrupamos los elementos que son similares:

$-3x=21$

Finalmente, despejamos la x pasando el -3 dividiendo al otro miembro de la ecuación y resolviendo la división:

$x=\cfrac{21}{-3}$

$\bm{x=-7}$

Ejercicio 8

Halla el valor de la x de la siguiente ecuación de primer grado con paréntesis anidados:

$3\left(x-2\right)-6=2\bigl[x-3\left(x-3\right)\bigr]+5$

Ver solución

La ecuación del problema se trata de una ecuación grado 1 formada por paréntesis anidados. De manera que primero resolveremos el paréntesis que está dentro de los corchetes:

$3\left(x-2\right)-6=2\bigl[x-3\cdot x-3 \cdot (-3)\bigr]+5$

$3\left(x-2\right)-6=2\bigl[x-3x+9\bigr]+5$

Y luego simplificamos los paréntesis restantes:

$3\cdot x-3 \cdot 2-6=2\cdot x+2\cdot (-3x)+2\cdot 9+5$

$3x-6-6=2x-6x+18+5$

Ahora pasamos los monomios al lado izquierdo de la ecuación y los elementos sin incógnita al derecho:

$3x-2x+6x=18+5+6+6$

Hacemos las sumas y las restas de cada miembro:

$7x=35$

Y, por último, hallamos la incógnita x:

$x=\cfrac{35}{7}$

$\bm{x=5}$

Ejercicio 9

Resuelve la siguiente ecuación de primer grado con paréntesis anidados:

$8x-3=6x+\Bigl\{7-4\bigl[3x-\left(5-2x\right)\bigr]\Bigr\}$

Ver solución

Consiste en una ecuación primer grado formada por varios paréntesis anidados, por lo que debemos ir resolviendo los paréntesis de dentro hacia fuera. Empezamos con el paréntesis, que como solo tiene un signo negativo delante simplemente tenemos que cambiar el signo de todos los elementos de su interior:

$8x-3=6x+\Bigl\{7-4\bigl[3x-5+2x\bigr]\Bigr\}$

En segundo lugar, quitamos los corchetes aplicando la propiedad distributiva:

$8x-3=6x+\Bigl\{7-4\cdot 3x-4\cdot (-5)-4\cdot 2x \Bigr\}$

$8x-3=6x+\Bigl\{7-12x+20-8x \Bigr\}$

Y solo queda simplificar las llaves. Estas tienen delante únicamente un signo positivo, por lo tanto, podemos quitar las llaves y los términos de su interior permanecen iguales:

$8x-3=6x+7-12x+20-8x$

Ahora transponemos los términos con incógnita a un lado de la ecuación y los términos independientes al otro lado:

$8x-6x+12x+8x=7+20+3$

Hacemos las sumas y las restas de los términos con el mismo grado:

$22x=30$

Pasamos dividiendo el 22 al otro miembro de la ecuación:

$x=\cfrac{30}{22}$

Y, por último, simplificamos la fracción dividendo el numerador y el denominador entre 2:

$\bm{x=}\mathbf{\cfrac{15}{11}}$

Ejercicio 10

Soluciona la siguiente ecuación de primer grado con paréntesis anidados:

$2x-\Bigl[4\left(3x-2\right)+\left(1-x\right)+5\left(x+3\right)\Bigr]=7-2\Bigl[x+2\left(4x+5\right)\Bigr]$

Ver solución

El problema corresponde a una ecuación de primer grado compuesta por paréntesis anidados. De modo que primero debemos calcular los paréntesis que están dentro de los corchetes usando la propiedad distributiva:

$2x-\Bigl[4\cdot 3x+4\cdot(-2)+1-x+5\cdot x+5\cdot 3\Bigr]=7-2\Bigl[x+2\cdot 4x+2\cdot 5\Bigr]$

$2x-\Bigl[12x-8+1-x+5x+15\Bigr]=7-2\Bigl[x+8x+10\Bigr]$

Y después resolvemos los corchetes:

$2x-12x+8-1+x-5x-15=7-2\cdot x-2\cdot 8x-2\cdot 10$

$2x-12x+8-1+x-5x-15=7-2x-16x-20$

Ahora pasamos los términos con incógnita al miembro izquierdo de la ecuación y los términos sin incógnita al miembro derecho:

$2x-12x+x-5x+2x+16x=7-20-8+1+15$

Agrupamos los términos similares de cada miembro:

$4x=-5$

Y, para acabar, despejamos la incógnita x:

$\bm{x=}\mathbf{\cfrac{-5}{4}}$

Ejercicio 11

Resuelve la siguiente ecuación de primer grado con fracciones:

$x- \cfrac{x+4}{5} = 1 + \cfrac{x}{2}$

Ver solución

En primer lugar, debemos encontrar el m.c.m. entre los denominadores de la ecuación lineal, que en este caso es 10:

$m.c.m.(2,5) = 10$

Por lo tanto, multiplicamos por 10 cada término de la ecuación para eliminar las fracciones:

$10 \cdot x- 10\cdot\cfrac{x+4}{5} = 10\cdot 1 +10 \cdot \cfrac{x}{2}$

Ahora simplificamos las fracciones dividiendo el 10 entre el denominador:

$10 \cdot x- 2 \cdot(x+4)= 10\cdot 1 + 5 \cdot x$

Calculamos las multiplicaciones:

$10x- 2x-8= 10 + 5x$

Pasamos los monomios a un lado y los términos independientes al otro lado:

$10x - 2x -5x = 8 +10$

Sumamos y restamos los términos de cada lado:

$3x= 18$

Y finalmente despejamos la incógnita x:

$x= \cfrac{18}{3}$

$\bm{x= 6}$

Ejercicio 12

Calcula la siguiente ecuación de primer grado con fracciones:

$\cfrac{x+10}{2} -\cfrac{x-20}{4} - \cfrac{x-30}{3} = 15$

Ver solución

Primero de todo, tenemos que averiguar el m.c.m. entre los denominadores de las fracciones, que en este problema es 12:

$m.c.m.(2,3,4) = 12$

De modo que multiplicamos por 12 cada término de la ecuación para quitar los denominadores:

$12\cdot\cfrac{x+10}{2} -12\cdot\cfrac{x-20}{4} - 12\cdot\cfrac{x-30}{3} = 12\cdot 15$

Simplificamos los denominadores dividiendo el 12 entre cada denominador:

$6\cdot(x+10) -3\cdot(x-20)- 4\cdot(x-30) = 12 \cdot 15$

Realizamos las multiplicaciones resultantes:

$6x+60- 3x+60 -4x +120= 180$

Pasamos los elementos con x a un lado de la ecuación y los números sin x al otro lado:

$6x -3x -4x = -60 -60 -120 +180$

Agrupamos los términos de cada lado:

$-x= -60$

Y, para terminar, despejamos x:

$x= \cfrac{-60}{-1}$

$\bm{x= 60}$

Ejercicio 13

Soluciona la siguiente ecuación de primer grado con fracciones:

$\cfrac{2x-10}{3} +2 - \cfrac{3(x-12)}{4} = 1$

Ver solución

El primer paso es hallar el m.c.m. entre los denominadores de la ecuación, que en este ejercicio es 12:

$m.c.m.(3,4) = 12$

Así debemos multiplicar por 12 cada elemento de la ecuación para quitar las fracciones:

$12 \cdot \cfrac{2x-10}{3} +12 \cdot 2 -12 \cdot \cfrac{3(x-12)}{4} = 12 \cdot 1$

Simplificamos las fracciones calculando la división entre 12 y cada denominador:

$4\cdot(2x-10) +12\cdot 2 -3\cdot 3(x-12) = 12\cdot 1$

Solucionamos las multiplicaciones:

$8x-40 + 24 - 9(x-12) = 12$

$8x-40+24-9x+108 = 12$

Movemos los términos con incógnita al miembro izquierdo de la ecuación y los términos sin incógnita al otro miembro:

$8x-9x=40-24-108+12$

Sumamos y restamos los términos de cada miembro:

$-x = -80$

Y, finalmente, hallamos la incógnita x:

$x= \cfrac{-80}{-1}$

$\bm{x= 80}$

Ejercicio 14

Halla la x de la siguiente ecuación de primer grado con fracciones:

$\cfrac{3-x}{7} -3x =\cfrac{3+2(x-1)}{14} -2x$

Ver solución

Lo primero que debemos hacer para solucionar una ecuación de este tipo es encontrar el mínimo común múltiplo de los denominadores, que en este problema es 14:

$m.c.m.(7,14) = 14$

Por lo tanto, multiplicamos cada término de la ecuación por el m.c.m. para quitar los denominadores:

$14\cdot \cfrac{3-x}{7} -14\cdot 3x =14\cdot \cfrac{3+2(x-1)}{14} -14\cdot 2x$

Luego simplificamos las fracciones dividiendo el 14 entre cada denominador:

$2(3-x) -14 \cdot 3x = 1\bigl[3+2(x-1)\bigr] - 14 \cdot 2x$

Hacemos todas las multiplicaciones:

$6-2x -42x = 1\cdot 3+1\cdot 2(x-1) - 28x$

$6-2x -42x = 3+2(x-1) - 28x$

$6-2x -42x = 3+2x-2 - 28x$

Ponemos los términos con x en un miembro y los términos independientes en el otro miembro:

$-2x -42x-2x+28x =-6+3-2$

Sumamos y restamos los términos semejantes (del mismo grado):

$-18x = -5$

Y, para acabar, solo nos queda despejar la incógnita x:

$x=\cfrac{-5}{-18}$

$\bm{x=} \mathbf{\cfrac{5}{18}}$

Ejercicio 15

Resuelve la siguiente ecuación de primer grado con denominadores y paréntesis:

$\displaystyle \frac{1}{3}+\frac{3}{5}\left(2x+3\right)=\frac{5}{6}\left(x+3\right)$

Ver solución

Antes de simplificar las fracciones, debemos eliminar los paréntesis. Y, para ello, debemos aplicar la propiedad distributiva:

$\displaystyle \frac{1}{3}+\frac{3\cdot 2x}{5}+\frac{3\cdot 3}{5}=\frac{5\cdot x}{6}+\frac{5\cdot 3}{6}$

$\displaystyle \frac{1}{3}+\frac{6x}{5}+\frac{9}{5}=\frac{5x}{6}+\frac{15}{6}$

Ahora sí, calculamos el mínimo común múltiplo de los denominadores:

$m.c.m.(3,5,6) = 30$

Multiplicamos cada término de la ecuación por el m.c.m. para así quitar los denominadores:

$\displaystyle 30\cdot \frac{1}{3}+30\cdot\frac{6x}{5}+30\cdot\frac{9}{5}=30\cdot\frac{5x}{6}+30\cdot\frac{15}{6}$

Simplificamos las fracciones dividiendo el 30 entre cada denominador:

$\displaystyle 10\cdot 1+6 \cdot 6x+6\cdot 9=5\cdot 5x+5\cdot 15$

Hacemos todas las multiplicaciones:

$10+36x+54=25x+75$

Pasamos los términos con x a un lado y los términos sin x al otro lado:

$36x-25x=75-54-10$

Agrupamos los términos de cada miembro:

$11x=11$

Y hallamos la x:

$x=\cfrac{11}{11}$

$\bm{x=1}$

Ejercicio 16

Soluciona la siguiente ecuación de primer grado con fracciones y paréntesis:

$\displaystyle 2-\frac{5}{4}=6x-\frac{4}{7}\left[5-\frac{1}{3}\left(4-9x\right)\right]$

Ver solución

Lo primero que debemos hacer es quitar los paréntesis y los corchetes de la ecuación. Por lo tanto, aplicamos la propiedad distributiva 2 veces para resolver los paréntesis y los corchetes:

$\displaystyle 2-\frac{5}{4}=6x-\frac{4}{7}\left[5-\frac{1}{3}\cdot 4-\frac{1}{3}\cdot (-9x)\right]$

$\displaystyle 2-\frac{5}{4}=6x-\frac{4}{7}\left[5-\frac{4}{3}+\frac{9x}{3}\right]$

$\displaystyle 2-\frac{5}{4}=6x-\frac{4}{7}\left[5-\frac{4}{3}+3x\right]$

$\displaystyle 2-\frac{5}{4}=6x-\frac{4}{7}\cdot 5-\frac{4}{7}\cdot \left(-\frac{4}{3}\right)-\frac{4}{7}\cdot 3x$

$\displaystyle 2-\frac{5}{4}=6x-\frac{20}{7}+\frac{16}{21}-\frac{12x}{7}$

En segundo lugar, determinamos el mínimo común múltiplo de los denominadores:

$m.c.m.(4,7,21) = 84$

Multiplicamos toda la ecuación por el m.c.m. para así luego poder quitar las fracciones:

$\displaystyle 84 \cdot 2-84 \cdot\frac{5}{4}=84 \cdot 6x-84 \cdot \frac{20}{7}+84 \cdot\frac{16}{21}-84 \cdot\frac{12x}{7}$

Eliminamos las fracciones resolviendo la división entre el 84 y cada denominador:

$\displaystyle 84 \cdot 2-21 \cdot 5=84 \cdot 6x-12\cdot 20+4\cdot 16-12 \cdot 12x$

Multiplicamos los términos:

$168-105=504x-240+64-144x$

Pasamos los términos con x al miembro izquierdo y los términos sin x al miembro derecho:

$-504x+144x=-168+105-240+64$

Sumamos y restamos los monomios de cada lado:

$-360x=-239$

Y, finalmente, despejamos la incógnita x:

$x=\cfrac{-239}{-360}$

$\bm{x=}\mathbf{\cfrac{239}{360}}$

Problemas de ecuaciones de primer grado

Problema 1

La suma del doble de un número más 8 es igual a 30. ¿Cuál es el número que cumple esta igualdad?

Ver solución

El primer paso para resolver un problema de ecuaciones de primer grado es identificar la incógnita. En este caso, la incógnita x es el número que buscamos:

$x=\text{n\'umero que buscamos}$

En segundo lugar, tenemos que plantear la ecuación de primer grado del problema. Algebraicamente, el doble de un número es 2x, por lo tanto, la ecuación del problema es:

$2x+8=30$

Ahora resolvemos la ecuación de primer grado:

$2x=30-8$

$2x=22$

$x=\cfrac{22}{2}$

$x=11$

De modo que el número que cumple la igualdad del problema es el número 11.

Problema 2

Si sumamos 12 a dos números seguidos, da como resultado 47. ¿Cuáles son estos dos números seguidos?

Ver solución

Si llamamos x a un número cualquiera, el número que le sigue será x+1. Así que los dos números que estamos buscando son x y x+1.

$\text{dos n\'umeros seguidos} \ \longrightarrow \ \begin{cases}x\\[2ex]x+1\end{cases}$

El enunciado del problema dice que al sumar los dos números seguidos más 12, se obtiene el número 47. Por lo tanto, la ecuación del problema será:

$x+(x+1)+12=47$

$x+x+1+12=47$

Una vez hemos logrado plantear la ecuación de primer grado, la resolvemos:

$x+x=-1-12+47$

$2x=34$

$x=\cfrac{34}{2}$

$x=17$

Por lo tanto, los dos números seguidos que buscamos son 17 y su siguiente número, esto es, 18.

$x=17$

$x+1=18$

Problema 3

La altura de un rectángulo mide 3 veces más que su base. Si el perímetro del rectángulo mide 96 cm, ¿cuáles son las dimensiones del rectángulo?

Ver solución

En este problema tenemos que calcular la base y la altura del rectángulo. Además, el enunciado nos dice que la altura es tres veces más grande que la base, de manera que si llamamos x a la base, la altura será:

$x=base$

$3x=altura$

Así pues, el perímetro de un rectángulo es la suma del doble de su base más el doble de su altura, por lo tanto:

$2x+2\cdot 3x=96$

Resolvemos la ecuación lineal obtenida:

$2x+6x=96$

$8x=96$

$x=\cfrac{96}{8}$

$x=12$

Así que el valor de la base y la altura del rectángulo serán:

$base=x=12 \ cm$

$altura=3x=3\cdot 12= 36 \ cm$

Problema 4

María tiene el triple de dinero que Miguel y entre los dos tienen en total 56€. ¿Cuánto dinero tiene cada uno?

Ver solución

Si decimos que x es el dinero que Miguel tiene, el dinero que tiene María será 3x, ya que María tiene tres veces más dinero que Miguel.

$x=\text{dinero de Miguel}$

$3x=\text{dinero de Mar\'ia}$

Si entre los dos suman 56€, significa que se cumple la siguiente ecuación de primer grado:

$x+3x=56$

Despejamos la x de ecuación de primer grado obtenida:

$4x=56$

$x=\cfrac{56}{4}$

$x=14$

En conclusión, Miguel tiene 14€ y María el triple, que es 42€.

$\text{dinero de Miguel}=x=14$

$\text{dinero de Mar\'ia}=3x=3\cdot 14=42$

Problema 5

Si un padre tiene 42 años y sus hijos 18 y 20 años, ¿cuántos años deben pasar para que la edad del padre sea la suma de las edades de sus hijos?

Ver solución

En este problema, la incógnita es los años que deben pasar para que se cumpla condición de edades del enunciado.

$x=\text{a\~nos que deben pasar}$

Entonces, para calcular la edad de alguien en el futuro, se debe sumar su edad actual más x. En consecuencia, la ecuación lineal del problema es:

$(42+x)=(18+x)+(20+x)$

$42+x=18+x+20+x$

Finalmente, hallamos el valor de x de la ecuación:

$x-x-x=-42+18+20$

$-x=-4$

$x=\cfrac{-4}{-1}$

$x=4$

De modo que deben pasar cuatro años para que la suma de las edades de los hijos sea equivalente a la edad del padre.

Problema 6

En una sala hay 451 personas. Además, se sabe que hay 47 mujeres más que hombres. ¿Cuántas mujeres y cuántos hombres hay en la sala?

Ver solución

Si llamamos x al número de hombres que hay en la sala, el número de mujeres será x+47:

$x=\text{n\'umero de hombres}$

$x+47=\text{n\'umero de mujeres}$

Así pues, el enunciado del problema dice que la suma del número de hombres y de mujeres da 451, lo que significa que se debe cumplir la siguiente igualdad:

$x+(x+47)=451$

$x+x+47=451$

Ahora solucionamos la ecuación de primer grado:

$x+x=-47+451$

$2x=404$

$x=\cfrac{404}{2}$

$x=202$

Y, por último, interpretamos la solución obtenida. En la sala hay 202 hombres, por otro lado, el número de mujeres es 202 más 47, es decir, 249 mujeres.

$\text{n\'umero de hombres}=x=202$

$\text{n\'umero de mujeres}=x+47=202+47=249$

Problema 7

En un parking de coches y motos hay 83 vehículos. Si en total se han contado 256 ruedas, ¿cuántos coches y cuántas motos hay en el parking?

Ver solución

Para resolver este problema, llamaremos x al número de coches que hay en el parking. De modo que el número de motos será la diferencia entre 83 y x.

$x=\text{n\'umero de coches}$

$83-x=\text{n\'umero de motos}$

Como sabes, un coche tiene cuatro ruedas y una moto tiene dos ruedas. Por lo tanto, si en el parking hay un total de 256 ruedas, se debe cumplir la siguiente ecuación:

$4x+2\cdot (83-x)=256$

Así pues, resolvemos la ecuación de primer grado con paréntesis del problema:

$4x+166-2x=256$

$4x-2x=256-166$

$2x=90$

$x=\cfrac{90}{2}$

$x=45$

En conclusión, en el parking hay 45 coches y, por otro lado, el número de motos es la diferencia entre 83 y 45, que es 38.

$\text{n\'umero de coches}=x=45$

$\text{n\'umero de motos}=83-x=83-45=38$

Problema 8

Un número aumentado en 9 unidades es igual al mismo número multiplicado por 4. ¿De qué número se trata?

Ver solución

En este caso, la incógnita del problema es el número que queremos hallar:

$x=\text{n\'umero que buscamos}$

Así pues, el enunciado nos dice que sumar 9 al número equivale a multiplicar dicho número por 4. Por lo tanto, se cumplirá la siguiente ecuación:

$x+9=4x$

Finalmente, resolvemos la ecuación de primer grado del problema:

$x-4x=-9$

$-3x=-9$

$x=\cfrac{-9}{-3}$

$x=3$

Problema 9

Hemos dejado el coche 6 horas en un parking. Si hemos pagado con un billete de 20€ y nos han dado de cambio 11€, ¿cuál es el precio por hora del parking?

Ver solución

En este problema queremos averiguar la tarifa del parking, así que la incógnita del problema será:

$x=\text{precio por hora del parking}$

A partir de la información del enunciado del problema, planteamos la ecuación de primer grado:

$20-6x=11$

Y, por último, resolvemos la ecuación:

$-6x=-20+11$

$-6x=-9$

$x=\cfrac{-9}{-6}$

$x=1,5$

De modo que el parking cobra 1,5€/hora por dejar el coche dentro.

Problema 10

Carlos hace una compra de 7€. Entonces, el doble del dinero que le queda más 4€ da justo el dinero que tenía al principio. ¿Cuántos euros tenía Carlos antes de hacer la compra?

Ver solución

La incógnita que queremos determinar en este problema es el dinero que tenía Carlos al principio.

$x=\text{dinero de Carlos al principio}$

Así pues, planteamos la ecuación de primer grado del problema con la información del enunciado:

$2(x-7)+4=x$

Finalmente, resolvemos la ecuación de primer grado con paréntesis del problema:

$2x-14+4=x$

$2x-x=14-4$

$x=10$

En conclusión, Carlos tenía al principio, antes de realizar la compra, 10€.

Ejercicios de ecuaciones de segundo grado completas

➤ Ver: cómo resolver ecuaciones de segundo grado

Ejercicio 17

Resuelve la siguiente ecuación de segundo grado completa:

$x^2-3x+2=0$

Ver solución

Se trata de una ecuación de segundo grado, por lo que tenemos que usar la fórmula general para resolverla:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Así pues, identificamos el valor de cada parámetro:

$\begin{array}{c}x^2-3x+2=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=-3\\[2ex]c=2\end{array}$

Ahora sustituimos el valor de cada parámetro en la fórmula general:

$\displaystyle x=\frac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1}$

Y hacemos los cálculos para hallar las dos soluciones de la ecuación de segundo grado:

$\begin{array}{l}\displaystyle x=\frac{3\pm \sqrt{9-8}}{2}\\[3ex]\displaystyle x=\frac{3\pm \sqrt{1}}{2}\\[3ex]\displaystyle x=\frac{3\pm 1}{2}=\begin{cases}\displaystyle\frac{3+1}{2}=\frac{4}{2}=2\\[4ex]\displaystyle\frac{3-1}{2}=\frac{2}{2}=1\end{cases}\end{array}$

Ejercicio 18

Calcula las soluciones de la siguiente ecuación de segundo grado:

$x^2+6x+8=0$

Ver solución

Para determinar las soluciones de la ecuación de segundo grado, tenemos que aplicar la fórmula general de este tipo de ecuaciones:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

De modo que primero debemos averiguar el valor de cada parámetro de la fórmula:

$\begin{array}{c}x^2+6x+8=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=6\\[2ex]c=8\end{array}$

Luego sustituimos el valor de cada parámetro en la fórmula de las ecuaciones de segundo grado:

$\displaystyle x=\frac{-6\pm \sqrt{6^2-4\cdot 1 \cdot 8}}{2\cdot 1}$

Por último, calculamos las operaciones resultantes para obtener las dos soluciones de la ecuación cuadrática:

$\begin{array}{l}\displaystyle x=\frac{-6\pm \sqrt{36-32}}{2}\\[3ex]\displaystyle x=\frac{-6\pm \sqrt{4}}{2}\\[3ex]\displaystyle x=\frac{-6\pm 2}{2}=\begin{cases}\displaystyle\frac{-6+2}{2}=\frac{-4}{2}=-2\\[4ex]\displaystyle\frac{-6-2}{2}=\frac{-8}{2}=-4\end{cases}\end{array}$

Ejercicio 19

Resuelve la siguiente ecuación cuadrática completa:

$2x^2+5x+6=0$

Ver solución

La fórmula general para resolver ecuaciones cuadráticas completas es la siguiente:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Así pues, el parámetro a es el coeficiente del término cuadrático, el parámetro b es el coeficiente del término lineal y el parámetro c es el término independiente de la ecuación:

$\begin{array}{c}2x^2+5x+6=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=2\\[2ex]b=5\\[2ex]c=6\end{array}$

Sustituimos el valor de cada parámetro en la fórmula general:

$\displaystyle x=\frac{-5\pm \sqrt{5^2-4\cdot 2 \cdot 6}}{2\cdot 2}$

Hacemos los cálculos:

$\begin{array}{l}\displaystyle x=\frac{-5\pm \sqrt{25-48}}{4}\\[3ex]\displaystyle x=\frac{-5\pm \sqrt{-24}\color{red}\bm{\times}\color{black}}{4} \ \end{array}$

Sin embargo, las raíces cuadradas de números negativos no tienen ninguna solución real, por lo tanto, la ecuación de segundo grado tampoco tiene ninguna solución real.

Ejercicio 20

Encuentra las soluciones de la siguiente ecuación cuadrática:

$\displaystyle 10x^2+3x-1=0$

Ver solución

La fórmula general de las ecuaciones cuadráticas es la siguiente:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

Así pues, identificamos cuánto vale cada parámetro de la fórmula:

$\begin{array}{c}10x^2+3x-1=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=10\\[2ex]b=3\\[2ex]c=-1\end{array}$

Sustituimos el valor de cada parámetro en la fórmula:

$\displaystyle x=\frac{-3\pm \sqrt{3^2-4\cdot 10 \cdot (-1)}}{2\cdot 10}$

Por último, hacemos los cálculos para encontrar las dos soluciones de la ecuación cuadrática:

$\begin{array}{l}\displaystyle x=\frac{-3\pm \sqrt{9+40}}{20}\\[3ex]\displaystyle x=\frac{-3\pm \sqrt{49}}{20}\\[3ex]\displaystyle x=\frac{-3\pm 7}{20}=\begin{cases}\displaystyle\frac{-3+7}{20}=\frac{4}{20}=\frac{1}{5}\\[4ex]\displaystyle\frac{-3-7}{20}=\frac{-10}{20}=-\frac{1}{2}\end{cases}\end{array}$

Ejercicio 21

Halla las soluciones de la siguiente ecuación de segundo grado:

$3x^2+2x-15+x=2x^2+4x-3$

Ver solución

Antes de utilizar la fórmula general, tenemos que simplificar los términos. Así que pasamos todos los términos al mismo miembro de la ecuación:

$3x^2-2x^2+2x+x-4x-15+3=0$

Y ahora sumamos los términos que tienen el mismo grado:

$x^2-x-12=0$

De este forma, una vez ya tenemos la ecuación simplificada, ya podemos emplear la fórmula general:

$\displaystyle x=\frac{-b\pm \sqrt{ b^2-4\cdot a \cdot c}}{2\cdot a}$

El valor de cada parámetro de la fórmula es el siguiente:

$\begin{array}{c}x^2-x-12=0\\[3ex]ax^2+bx+c=0\end{array}\ \color{orange} \bm{\longrightarrow}\color{black}\begin{array}{c}a=1\\[2ex]b=-1\\[2ex]c=-12\end{array}$

Sustituimos el valor de cada parámetro en la fórmula:

$\displaystyle x=\frac{-(-1)\pm \sqrt{(-1)^2-4\cdot 1 \cdot (-12)}}{2\cdot 1}$

Y, finalmente, calculamos las dos soluciones de la ecuación de segundo grado:

$\begin{array}{l}\displaystyle x=\frac{1\pm \sqrt{1+48}}{2}\\[3ex]\displaystyle x=\frac{1\pm \sqrt{49}}{2}\\[3ex]\displaystyle x=\frac{1\pm 7}{2}=\begin{cases}\displaystyle\frac{1+7}{2}=\frac{8}{2}=4\\[4ex]\displaystyle\frac{1-7}{2}=\frac{-6}{2}=-3\end{cases}\end{array}$

Ejercicio 22

Resuelve la siguiente ecuación de segundo grado con paréntesis:

$2x-\left(x^2+5x-4\right)=3\left(2x+4\right)$

Ver solución

En primer lugar, tenemos que quitar los paréntesis y, para ello, debemos aplicar la propiedad distributiva:

$2x-x^2-5x+4=3\cdot 2x+3 \cdot 4$

$2x-x^2-5x+4=6x+12$

Luego colocamos todos los monomios en el miembro izquierdo de la ecuación:

$2x-x^2-5x+4-6x-12=0$

Agrupamos los términos con el mismo grado:

$-x^2-9x-8=0$

Y, finalmente, utilizamos la fórmula de la ecuación de segundo grado:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-(-9)\pm \sqrt{(-9)^2-4\cdot (-1)\cdot (-8)}}{2\cdot (-1)} = \\[2ex] & = \cfrac{+9 \pm \sqrt{81-32}}{-2} = \\[2ex] &= \cfrac{9 \pm \sqrt{49}}{-2}= \\[1.5ex] & =\cfrac{9 \pm 7}{-2} = \begin{cases} \cfrac{9+ 7}{-2} =\cfrac{16}{-2} = \bm{-8} \\[3ex] \cfrac{9-7}{-2} =\cfrac{2}{-2} = \bm{-1}\end{cases} \end{aligned}$

Ejercicio 23

Soluciona la siguiente ecuación de segundo grado con paréntesis y corchetes:

$2\bigl[x^2-4x\left(x+3\right)\bigr]-7=3x+5$

Ver solución

El primer paso del procedimiento consiste en eliminar todos los paréntesis. Pero en este problema tenemos un paréntesis dentro de un corchete, por lo que tenemos que aplicar la propiedad distributiva dos veces:

$2\bigl[x^2-4x\cdot x+4x\cdot 3\bigr]-7=3x+5$

$2\bigl[x^2-4x^2-12x \bigr]-7=3x+5$

$2\cdot x^2+2\cdot (-4x^2)+2\cdot (-12x) -7=3x+5$

$2x^2-8x^2-24x -7=3x+5$

Trasponemos todos los elementos al miembro izquierdo de la ecuación:

$2x^2-8x^2-24x -7-3x-5=0$

Sumamos y restamos los términos con el mismo grado:

$-6x^2-27x-12=0$

En este problema tenemos una ecuación de segundo grado completa, así que aplicamos la fórmula general de la ecuación cuadrática:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-(-27)\pm \sqrt{(-27)^2-4\cdot (-6)\cdot (-12)}}{2\cdot (-6)} = \\[2ex] & = \cfrac{+27 \pm \sqrt{729-288}}{-12} = \\[2ex] &= \cfrac{27 \pm \sqrt{441}}{-12}= \\[1.5ex] & =\cfrac{27 \pm 21}{-12} = \begin{cases} \cfrac{27+21}{-12}=\cfrac{48}{-12}= \bm{-4} \\[3ex] \cfrac{27-21}{-12}=\cfrac{6}{-12}= \bm{-}\mathbf{\cfrac{1}{2}}\end{cases} \end{aligned}$

Ejercicio 24

Resuelve la siguiente ecuación de segundo grado con fracciones:

$\cfrac{x^2}{2}+\cfrac{x}{2}=\cfrac{2x^2+1}{3}$

Ver solución

En primer lugar, calculamos el mínimo común múltiplo de los denominadores:

$m.c.m.(2,3) = 6$

Luego multiplicamos cada término de la ecuación por el valor hallado del mínimo común múltiplo:

$6\cdot \cfrac{x^2}{2}+6\cdot \cfrac{x}{2}=6\cdot \cfrac{2x^2+1}{3}$

Simplificamos las fracciones dividiendo el 6 entre cada denominador:

$3\cdot x^2+3\cdot x =2\cdot (2x^2+1)$

Multiplicamos:

$3x^2+3x =2\cdot 2x^2+2 \cdot 1$

$3x^2+3x =4x^2+2$

Pasamos todos los monomios al primer miembro de la ecuación:

$3x^2+3x -4x^2-2=0$

Y agrupamos los términos del mismo grado:

$-x^2+3x -2=0$

De forma que hemos obtenido una ecuación de segundo grado completa, así que utilizamos la fórmula general para resolverla:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-3\pm \sqrt{3^2-4\cdot (-1) \cdot (-2)}}{2\cdot (-1)} = \\[2ex] & = \cfrac{-3 \pm \sqrt{9-8}}{-2} = \\[2ex] &= \cfrac{-3 \pm \sqrt{1}}{-2}= \\[1.5ex] & =\cfrac{-3 \pm 1}{-2}= \begin{cases} \cfrac{-3 + 1}{-2}=\cfrac{-2}{-2} =\bm{1}\\[3ex]\cfrac{-3-1}{-2}=\cfrac{-4}{-2} =\bm{2} \end{cases} \end{aligned}$

Ejercicio 25

Calcula la siguiente ecuación cuadrática con fracciones:

$\cfrac{x^2-3}{4}+\cfrac{x}{3}=-1-\cfrac{x}{2}$

Ver solución

Primero de todo, debemos averiguar el mínimo común múltiplo de los denominadores de las fracciones, que en este problema es 12:

$m.c.m.(2,3,4) = 12$

Por lo que multiplicamos cada término de la ecuación por 12:

$12\cdot \cfrac{x^2-3}{4}+12\cdot \cfrac{x}{3}=-12\cdot 1-12\cdot \cfrac{x}{2}$

Simplificamos las fracciones de la ecuación dividiendo el 12 entre cada denominador:

$3 \cdot (x^2-3)+4\cdot x=-12\cdot 1-6\cdot x$

Resolvemos las multiplicaciones:

$3\cdot x^2+3\cdot (-3)+4x=-12-6x$

$3x^2-9+4x=-12-6x$

Movemos todos los términos al miembro izquierdo de la ecuación:

$3x^2-9+4x+12+6x=0$

Agrupamos los términos semejantes:

$3x^2+10x+3=0$

Y, finalmente, aplicamos la fórmula general de las ecuaciones cuadráticas:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-10\pm \sqrt{10^2-4\cdot 3 \cdot 3}}{2\cdot 3} = \\[2ex] & = \cfrac{-10 \pm \sqrt{100-36}}{6} = \\[2ex] &= \cfrac{-10 \pm \sqrt{64}}{6}= \\[1.5ex] & =\cfrac{-10 \pm 8}{6}= \begin{cases} \cfrac{-10 + 8}{6} =\cfrac{-2}{6} =\bm{-}\mathbf{\cfrac{1}{3}}\\[3ex]\cfrac{-10-8}{6} =\cfrac{-18}{6} =\bm{-3} \end{cases} \end{aligned}$

Ejercicio 26

Soluciona la siguiente ecuación de segundo grado con fracciones y paréntesis:

$\cfrac{3x^2}{4}+\cfrac{2}{3}\left(x-5\right)=1$

Ver solución

La ecuación del problema es de grado 2 (porque tiene una x elevada al cuadrado) y está formada por fracciones y paréntesis. Por tanto, lo primero que debemos hacer es operar los paréntesis aplicando la propiedad distributiva:

$\cfrac{3x^2}{4}+\cfrac{2}{3}\cdot x+\cfrac{2}{3}\cdot(-5)=1$

$\cfrac{3x^2}{4}+\cfrac{2x}{3}-\cfrac{10}{3}=1$

Una vez hemos simplificado los paréntesis, calculamos el mínimo común múltiplo de los denominadores:

$m.c.m.(3,4) = 12$

Ahora multiplicamos toda la ecuación por el mcm hallado:

$12 \cdot \cfrac{3x^2}{4}+12 \cdot\cfrac{2x}{3}-12 \cdot\cfrac{10}{3}=12 \cdot 1$

Simplificamos las fracciones de la ecuación dividiendo el 12 entre cada denominador:

$3 \cdot 3x^2+4 \cdot 2x-4 \cdot 10=12 \cdot 1$

Hallamos las multiplicaciones:

$9x^2+8x-40=12$

Trasponemos los términos necesarios para que todos queden en el primer miembro de la ecuación:

$9x^2+8x-40-12=0$

Sumamos y restamos los términos semejantes:

$9x^2+8x-52=0$

Y, por último, empleamos fórmula de la ecuación de segundo grado:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-8\pm \sqrt{8^2-4\cdot 9 \cdot (-52)}}{2\cdot 9} = \\[2ex] & = \cfrac{-8\pm \sqrt{64+1872}}{18} = \\[2ex] &= \cfrac{-8 \pm \sqrt{1936}}{18}= \\[1.5ex] & =\cfrac{-8 \pm 44}{18}= \begin{cases} \cfrac{-8 +44}{18}=\cfrac{36}{18}=\bm{2} \\[3ex] \cfrac{-8-44}{18}=\cfrac{-52}{18}=\bm{-}\mathbf{\cfrac{26}{9}} \end{cases} \end{aligned}$

Ejercicios de ecuaciones de segundo grado incompletas

➤ Ver: cómo resolver ecuaciones de segundo grado incompletas

Ejercicio 27

Resuelve la siguiente ecuación de segundo grado incompleta:

$x^2-9 = 0$

Ver solución

Se trata de una ecuación de segundo grado incompleta con ausencia del término b, por lo tanto, primero despejamos la incógnita:

$x^2=9$

Y luego hacemos la raíz cuadrada en ambos miembros de la ecuación:

$\sqrt{x^2}=\sqrt{9}$

$x=\pm 3$

De modo que las dos soluciones de la ecuación de segundo grado incompleta son +3 y -3.

$\bm{x=+3} \qquad \bm{x=-3}$

Ejercicio 28

Calcula la siguiente ecuación cuadrática incompleta:

$4x^2-4 = 0$

Ver solución

A la ecuación de segundo grado incompleta le falta el coeficiente b, en consecuencia, primero tenemos que despejar el término cuadrático. Así que pasamos al otro lado el -4 cambiándole el signo:

$4x^2=4$

En segundo lugar, pasamos el coeficiente de x² al otro miembro dividiendo:

$x^2=\cfrac{4}{4}$

$x^2=1$

Y, por último, sacamos la raíz cuadrada de ambos miembros de la igualdad:

$\sqrt{x^2}=\sqrt{1}$

$x= \pm 1$

Por lo que las dos soluciones de la ecuación cuadrática incompleta son +1 y -1:

$\bm{x=+1} \qquad \bm{x=-1}$

Ejercicio 29

Soluciona la siguiente ecuación de segundo grado incompleta:

$4x^2+20x=0$

Ver solución

A la ecuación de segundo grado incompleta le falta el coeficiente c. Por lo tanto, primero tenemos que sacar el factor común x de la ecuación:

$x(4x+20) = 0$

Después igualamos cada factor del producto anterior a cero:

$\displaystyle x(4x+20) = 0 \begin{cases} x=0 \\[2ex] 4x+20=0 \end{cases}$

Ahora ya sabemos que una de las soluciones de la ecuación será x=0. Pues ara hallar la otra solución resolvemos la ecuación lineal resultante del paso anterior:

$4x+20= 0$

$4x=-20$

$x=\cfrac{-20}{4}$

$x=-5$

En definitiva, las dos soluciones de la ecuación son:

$\bm{x=0} \qquad \bm{x=-5}$

Ejercicio 30

Determina la siguiente ecuación de segundo grado incompleta:

$5x^2-15x=0$

Ver solución

A la ecuación cuadrática incompleta le falta el coeficiente c. Por lo tanto, primero extraemos el factor común x de la ecuación:

$x(5x-15) = 0$

Igualamos cada factor de la multiplicación anterior a cero:

$\displaystyle x(5x-15) = 0 \begin{cases} x=0 \\[2ex] 5x-15=0 \end{cases}$

Con lo que una de las soluciones de la ecuación será x=0. Entonces, resolvemos la ecuación de primer grado obtenida en el paso anterior para determinar la otra solución:

$5x-15= 0$

$5x=15$

$x=\cfrac{15}{5}$

$x=3$

Por tanto, las dos soluciones de la ecuación cuadrática incompleta son:

$\bm{x=0} \qquad \bm{x=3}$

Ejercicio 31

Resuelve la siguiente ecuación de grado 2 incompleta:

$10x^2 = 0$

Ver solución

En este problema a la ecuación de segundo grado incompleta le falta tanto el coeficiente b como el coeficiente c, lo que significa que las dos soluciones de la ecuación son x=0 (solución doble).

$\bm{x=0} \qquad \bm{x=0}$

Ejercicio 32

Halla la x de la siguiente ecuación de segundo grado incompleta:

$2x^2+50 = 0$

Ver solución

La ecuación de segundo grado incompleta no tiene término lineal, así que despejamos el término de grado 2:

$2x^2=-50$

$x^2=\cfrac{-50}{2}$

$x^2=-25$

Y ahora tendríamos que calcular la raíz cuadrada en ambos miembros de la igualdad:

$\sqrt{x^2}=\sqrt{-25}\color{red} \ \bm{\times}$

Sin embargo, la raíz cuadrada de un número real negativo no existe, por lo que la ecuación de segundo grado no tiene solución.

En realidad, sí que se pueden calcular las raíces cuadradas de números negativos, pero para eso es necesario tener un conocimiento de matemáticas más avanzado, ya que deberíamos resolver una ecuación de segundo grado incompleta con soluciones complejas.

Ejercicio 33

Resuelve la siguiente ecuación cuadrática incompleta con paréntesis:

$7x^2+2(3x-20)= 6(x+10)+3x^2$

Ver solución

Para determinar qué tipo de ecuación de segundo grado es, primero tenemos que operar los paréntesis. Y, para ello, aplicamos la propiedad distributiva:

$7x^2+2\cdot 3x+2\cdot (-20)= 6\cdot x+6\cdot 10+3x^2$

$7x^2+6x-40= 6x+60+3x^2$

Ahora pasamos todos los términos al lado izquierdo de la ecuación:

$7x^2+6x-40- 6x-60-3x^2=0$

Y agrupamos los términos semejantes:

$4x^2-100=0$

De manera que se anula el coeficiente b y, por tanto, se trata de una ecuación de segundo grado incompleta sin término lineal. Así que despejamos el término cuadrático:

$4x^2=100$

$x^2=\cfrac{100}{4}$

$x^2=25$

Y, por último, efectuamos la raíz cuadrada en ambos miembros de la ecuación:

$\sqrt{x^2}=\sqrt{25}$

$x= \pm 5$

Con lo que las dos soluciones de la ecuación de segundo grado incompleta son +5 y -5:

$\bm{x=+5} \qquad \bm{x=-5}$

Ejercicio 34

Resuelve la siguiente ecuación de segundo grado incompleta con fracciones y paréntesis:

$\cfrac{7x}{3}+\cfrac{3\left(x^2+4\right)}{4}=3+\cfrac{5x}{2}$

Ver solución

Para quitar las fracciones de la ecuación, primero debemos multiplicar cada uno de sus términos por el mínimo común múltiplo (m.c.m.) de sus denominadores (3,4 y 2), que en este caso es 12.

$12 \cdot \cfrac{7x}{3}+12 \cdot\cfrac{3\left(x^2+4\right)}{4}=12 \cdot 3+12 \cdot\cfrac{5x}{2}$

Ahora dividimos el 12 entre cada denominador para eliminar las fracciones:

$4 \cdot 7x+3 \cdot\bigl[3\left(x^2+4\right)\bigr]=12 \cdot 3+6 \cdot 5x$

Resolvemos los corchetes y los paréntesis utilizando la propiedad distributiva:

$4 \cdot 7x+3 \cdot\bigl[3x^2+12\bigr]=12 \cdot 3+6 \cdot 5x$

$4 \cdot 7x+9x^2+36=12 \cdot 3+6 \cdot 5x$

Multiplicamos:

$28x+9x^2+36=36+30x$

Una vez hemos simplificado las fracciones y los paréntesis de la ecuación cuadrática, pasamos todos los monomios al mismo miembro:

$28x+9x^2+36-36-30x=0$

Y sumamos (o restamos) los términos del mismo grado:

$9x^2-2x=0$

Por lo tanto, a la ecuación cuadrática incompleta le falta el coeficiente c. Así que sacamos el factor común x de la ecuación:

$x(9x-2) = 0$

Luego igualamos cada factor de la multiplicación anterior a cero:

$\displaystyle x(9x-2) = 0 \begin{cases} x=0 \\[2ex] 9x-2=0 \end{cases}$

De manera que una de las soluciones de la ecuación será x=0, y la otra la calculamos resolviendo la ecuación de primer grado obtenida :

$9x-2= 0$

$9x=2$

$\bm{x=}\mathbf{\cfrac{2}{9}}$

En conclusión, las 2 soluciones de la ecuación de segundo grado incompleta son:

$\bm{x=0} \qquad \bm{x=}\mathbf{\cfrac{2}{9}}$

Ejercicio 35

Calcula la siguiente ecuación cuadrática incompleta con paréntesis:

$5x\left(2x+6\right)-2x^2-3x=7x+4\left(x^2+5x+4\right)$

Ver solución

Primero de todo operamos los paréntesis con la propiedad distributiva:

$5x\cdot 2x+5x\cdot 6-2x^2-3x=7x+4\cdot x^2+4\cdot 5x+4\cdot 4$

$10x^2+30x-2x^2-3x=7x+4x^2+20x+16$

Luego ponemos todos los elementos en el lado izquierdo de la ecuación:

$10x^2+30x-2x^2-3x-7x-4x^2-20x-16=0$

Sumamos y restamos los términos semejantes:

$4x^2-16=0$

En este problema tenemos una ecuación de segundo grado incompleta sin término de primer grado, por lo tanto, no tenemos que aplicar la fórmula general sino despejar la incógnita x:

$4x^2=16$

$x^2=\cfrac{16}{4}$

$x^2=4$

Y, por último, hacemos la raíz cuadrada de ambos miembros de la ecuación:

$\sqrt{x^2}=\sqrt{4}$

$\bm{x=\pm 2}$

Así que las soluciones de la ecuación cuadrática son +2 y -2.

Ejercicio 36

Resuelve la siguiente ecuación de segundo grado incompleta con fracciones, paréntesis y corchetes:

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}-\frac{1}{6}\left[x-2\left(4+\frac{x}{2}\right)\right]$

Ver solución

La ecuación de este problema es de bastante dificultad, ya que combina fracciones, paréntesis y corchetes. Pero vamos paso por paso: primero tenemos que resolver los paréntesis y los corchetes utilizando la propiedad distributiva:

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}-\frac{1}{6}\left[x-2\cdot 4-2\cdot\frac{x}{2}\right]$

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}-\frac{1}{6}\left[x-8-x\right]$

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}-\frac{1}{6}\left[-8\right]$

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}-\frac{1}{6}\cdot (-8)$

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}+\frac{8}{6}$

Ahora tendríamos que encontrar el mínimo común múltiplo de los denominadores, sin embargo, antes podemos simplificar la última fracción, lo que nos facilitará los cálculos:

$\displaystyle -\frac{2}{3}+\frac{x^2}{2}=\frac{2x^2}{5}+\frac{4}{3}$

De esta forma tenemos que calcular el mínimo común múltiplo de menos números:

$m.c.m.(2,3,5) = 30$

Luego multiplicamos toda la ecuación por el mcm hallado:

$\displaystyle -30\cdot \frac{2}{3}+30 \cdot\frac{x^2}{2}=30 \cdot\frac{2x^2}{5}+30 \cdot\frac{4}{3}$

Simplificamos las fracciones de la ecuación dividiendo el 15 entre cada denominador:

$\displaystyle -10 \cdot 2+15 \cdot x^2=6 \cdot 2x^2+10 \cdot 4$

Resolvemos las multiplicaciones resultantes:

$\displaystyle -20+15x^2=12x^2+40$

Colocamos todos los términos en el primer miembro de la ecuación:

$\displaystyle -20+15x^2-12x^2-40=0$

Sumamos y restamos los términos del mismo grado:

$\displaystyle 3x^2-60=0$

Y, finalmente, resolvemos la ecuación de segundo grado incompleta:

$\displaystyle 3x^2-60=0$

$\displaystyle 3x^2=60$

$\displaystyle x^2=\cfrac{60}{3}$

$\displaystyle x^2=20$

$\displaystyle \bm{x=\pm\sqrt{20}}$

Problemas de ecuaciones de segundo grado

Problema 11

La multiplicación de un número por su doble da 288. ¿Qué número es?

Ver solución

Lo primero que debemos hacer es identificar la incógnita del problema. En este caso, x es el número que queremos hallar:

$x = \text{n\'umero que buscamos}$

En segundo lugar, debemos plantear la ecuación de segundo grado del problema. Para ello, primero debemos expresar algebraicamente el doble del número:

$\text{doble del n\'umero que buscamos} = 2x$

El enunciado del problema nos dice que el número incógnita multiplicado por su doble es igual a 288, por tanto:

$x \cdot 2x =288$

Y, finalmente, resolvemos la ecuación de segundo grado incompleta del problema:

$2x^2 =288$

$x^2 = \cfrac{288}{2}$

$x^2 = 144$

$x = \pm \sqrt{144}$

$\bm{x = \pm 12}$

Por lo tanto, el número que buscamos puede ser dos opciones: 12 o -12. En este problema, la solución negativa también está bien, ya que en ningún caso el problema nos dice que el número debe ser positivo.

Problema 12

Marta tiene el triple de edad que Juan. Y si multiplicamos sus edades obtenemos el resultado de 48. ¿Qué edad tiene cada uno?

Ver solución

La incógnita del problema tiene que ser o la edad de Juan, o la edad de Marta. Aquí lo hemos resuelto con la edad de Juan, pero también se podría plantear el problema escogiendo la edad de Marta como incógnita.

$x = \text{edad de Juan}$

El enunciado del problema dice que Marta tiene el triple de edad que Juan. Por lo tanto, la edad de Marta corresponde a la siguiente expresión:

$3x = \text{edad de Marta}$

Entonces, el problema dice que el resultado de multiplicar las dos edades es igual a 48. Por lo tanto:

$\text{edad de Juan} \cdot \text{edad de Marta} = 48$

$x \cdot 3x = 48$

Una vez hemos encontrado la ecuación cuadrática del problema, la resolvemos:

$3x^2 = 48$

$x^2 = \cfrac{48}{3}$

$x^2 = 16$

$x= \pm \sqrt{16}$

$x= \pm 4$

Así pues, las dos posibles soluciones son +4 y -4. Pero, evidentemente, una edad no puede ser negativa, por lo que la única solución factible es +4.

De forma que las edades son:

$\text{edad de Juan} = x = \mathbf{4 \ a\~nos}$

$\text{edad de Marta} = 3x = 3 \cdot 4 = \mathbf{12 \ a\~nos}$

Problema 13

Hallar un número cuyo doble más su cuadrado da 195.

Ver solución

En este problema la única incógnita posible es el número que queremos calcular:

$x= \text{n\'umero que buscamos}$

Matemáticamente, el doble del número que buscamos y su cuadrado son:

$2x = \text{doble del n\'umero}$

$x^2 = \text{cuadrado del n\'umero}$

El enunciado explica que la suma del doble del número más su cuadrado es igual a 195, por lo tanto, la ecuación del problema es:

$2x+x^2=195$

Así que resolvemos la ecuación de segundo grado completa del problema aplicando la fórmula general:

$x^2+2x-195=0$

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-2\pm \sqrt{2^2-4\cdot 1 \cdot (-195)}}{2\cdot 1} = \\[2ex] & = \cfrac{-2\pm \sqrt{4+780}}{2} = \\[2ex] &= \cfrac{-2 \pm \sqrt{784}}{2}= \\[1.5ex] & =\cfrac{-2 \pm 28}{2} = \begin{cases} \cfrac{-2 + 28}{2}=\cfrac{26}{2}=\bm{13} \\[3ex] \cfrac{-2- 28}{2}=\cfrac{-30}{2}=\bm{-15} \end{cases} \end{aligned}$

En este problema, el enunciado no especifica el signo del número, de manera que puede ser tanto +13 como -15. De hecho, si sustituimos las dos soluciones en la ecuación cuadrática del problema, podemos comprobar que ambas soluciones cumplen con la ecuación.

Problema 14

La longitud de un campo de fútbol hace 30 metros más que de anchura. Y su área es de 7000 m². ¿Cuáles son las dimensiones del campo?

Ver solución

En primer lugar, identificamos la incógnita del problema. En este caso diremos que x es igual a los metros de ancho del campo, pero también se podría solucionar poniendo como incógnita la longitud del campo.

$x = \text{metros de ancho del campo}$

Así pues, el problema dice que la longitud del campo mide 30 metros más que su ancho, por tanto:

$x +30 = \text{metros de longitud del campo}$

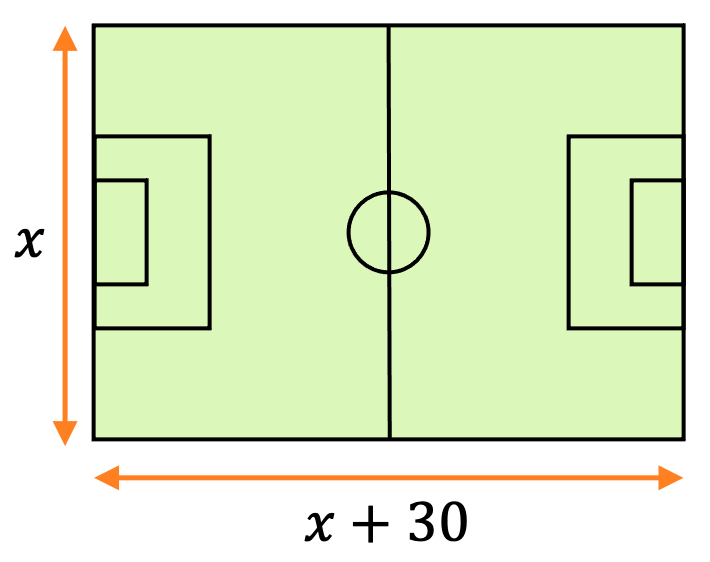
Problemas con ecuaciones de segundo grado con una incognita

Asimismo, el problema dice que el área del campo es 7000 m², por lo tanto, la ecuación cuadrática del problema es:

$A = b\cdot h$

$(x+30)\cdot x =7000$

$x^2+30x =7000$

Por último, resolvemos la ecuación cuadrática del problema:

$x^2+30x -7000=0$

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-30\pm \sqrt{30^2-4\cdot 1 \cdot (-7000)}}{2\cdot 1} = \\[2ex] & = \cfrac{-30\pm \sqrt{900+28000}}{2} = \\[2ex] &= \cfrac{-30 \pm \sqrt{28900}}{2}= \\[1.5ex] & =\cfrac{-30 \pm 170}{2} = \begin{cases} \cfrac{-30+170}{2}=\cfrac{140}{2} = 70 \\[3ex]\cfrac{-30-170}{2}=\cfrac{-200}{2} = -100 \end{cases} \end{aligned}$

En este problema, la interpretación de las soluciones obtenidas es importante, porque una dimensión de un campo no puede ser negativa. De modo que la única solución factible es x=70.

$\text{Ancho del campo} =x = \bm{70 \ m}$

$\text{Longitud del campo}=x+30=70+30=\bm{100 \ m}$

Problema 15

Al aumentar el lado de un cuadrado en 2 m, su área se cuadriplica. ¿Cuánto mide el lado original del cuadrado?

Ver solución

En este problema la incógnita será la longitud del lado del cuadrado original:

$x = \text{lado original del cuadrado}$

Como el área de un cuadrado se calcula multiplicando sus lados entre sí, el área original del cuadrado era:

$A=L\cdot L$

$x \cdot x = x^2 = \text{\'area del cuadrado original}$

El enunciado nos dice que si aumentamos 2 m la longitud del lado, su área se multiplica por 4. Por lo tanto, la ecuación de segundo grado del problema es:

$(x+2)\cdot (x+2)= 4\cdot x^2$

Ahora operamos los paréntesis aplicando la propiedad distributiva y agrupamos los términos semejantes:

$x^2+2x+2x+4= 4x^2$

$x^2+2x+2x+4-4x^2=0$

$-3x^2+4x+4=0$

Y solucionamos la ecuación cuadrática del problema utilizando la fórmula general:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{4\pm \sqrt{4^2-4\cdot (-3) \cdot 4}}{2\cdot (-3)} = \\[2ex] & = \cfrac{4\pm \sqrt{16+48}}{-6} = \\[2ex] &= \cfrac{4 \pm \sqrt{64}}{-6}= \\[1.5ex] & =\cfrac{4 \pm 16}{-6} = \begin{cases}\cfrac{4+16}{-6} =\cfrac{20}{-6} = -\cfrac{10}{3} \\[3ex]\cfrac{4-16}{-6} =\cfrac{-12}{-6} = 2\end{cases} \end{aligned}$

Lógicamente, la longitud inicial del cuadrado no podía ser negativa, por lo que la única solución posible es x=2.

$\text{Lado original del cuadrado} =x = \bm{2 \ m}$

Problema 16

Determina dos números positivos que se diferencian en 6 unidades y su producto es igual a 112.

Ver solución

Aunque el planteamiento de este problema se podría solucionar con dos incógnitas, para no tener que calcular un sistema de ecuaciones vamos a resolverlo mediante una ecuación de segundo grado con una sola incógnita.

En este caso llamaremos x al número más grande de los dos:

$x= \text{n\'umero grande}$

Como la diferencia entre los dos números es de 6 unidades, el otro número será:

$x-6= \text{n\'umero peque\~no}$

El producto de los dos números debe ser 112, por lo tanto:

$x\cdot (x-6)=112$

Eliminamos el paréntesis aplicando la propiedad distributiva:

$x^2-6x=112$

Y, por último, resolvemos la ecuación de segundo grado:

$x^2-6x-112=0$

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-(-6)\pm \sqrt{(-6)^2-4\cdot 1 \cdot (-112)}}{2\cdot 1} = \\[2ex] & = \cfrac{+6\pm \sqrt{36+448}}{2} = \\[2ex] &= \cfrac{6 \pm \sqrt{484}}{2}= \\[1.5ex] & =\cfrac{6 \pm 22}{2} = \begin{cases} \cfrac{6+22}{2}=\cfrac{28}{2}=14 \\[3ex] \cfrac{6-22}{2}=\cfrac{-16}{2}=-8 \end{cases} \end{aligned}$

En este problema, el enunciado solo admite números positivos. En consecuencia, la única solución factible del problema es:

$\text{n\'umero grande}=x=\bm{14}$

$\text{n\'umero peque\~no}=x-6=14-6=\bm{8}$

Problema 17

Si aumentamos la base de un cuadrado 25 cm y disminuimos su altura en 24 cm, obtenemos un rectángulo con la misma área. Calcula cuánto mide el lado del cuadrado.

Ver solución

La incógnita del problema se trata del dato que queremos calcular, esto es, el lado del cuadrado:

$x = \text{lado del cuadrado}$

De forma que los lados del rectángulo serán:

$\text{base rect\'angulo} = x+25$

$\text{altura rect\'angulo} = x-24$

Tanto el área de un cuadrado como la de un rectángulo se calculan con las siguientes fórmulas:

$A_{cuadrado}=L\cdot L = x \cdot x$

$A_{rect\'angulo}=b\cdot h =(x+25)\cdot (x-24)$

Por lo tanto, si ambas áreas deben ser iguales, se debe verificar la siguiente igualdad:

$A_{cuadrado}=A_{rect\'angulo}$

$x \cdot x=(x+25)\cdot (x-24)$

Hacemos las multiplicaciones:

$x^2=x^2-24x+25x-600$

Y resolvemos la ecuación de segundo grado del problema:

$x^2-x^2+24x-25x+600=0$

$-x+600=0$

En este problema las dos incógnitas elevadas al cuadrado se anulan, por lo que simplemente tenemos que despejar la x de la ecuación de primer grado resultante:

$600=x$

En definitiva, el lado del cuadrado mide 600 cm.

$\text{Lado del cuadrado} =x = \bm{600 \ cm}$

Problema 18

Determina cuánto miden los catetos de un triángulo rectángulo si juntos suman 17 cm y su hipotenusa mide 13 cm.

Ver solución

Para este problema llamaremos x a un cateto del triángulo

$x = \text{longitud de un cateto}$

De modo que si la longitud de los dos catetos suman 17 cm, el otro cateto debe medir:

$x+\text{longitud del otro cateto} = 17$

$\text{longitud del otro cateto} = 17-x$

problemas con ecuaciones de segundo grado para secundaria eso

Ahora podemos encontrar una ecuación que relaciona los tres lados del triángulo aplicando el teorema de Pitágoras:

$h^2=c^2+c^2$

$13^2=x^2+(17-x)^2$

Resolvemos la identidad notable con la fórmula de una resta al cuadrado:

$13^2=x^2+17^2-2\cdot 17\cdot x+x^2$

$169=x^2+289-34x+x^2$

Operamos:

$169-x^2-289+34x-x^2=0$

$-2x^2+34x-120=0$

Y, finalmente, resolvemos la ecuación de segundo grado del problema usando la fórmula general:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-34\pm \sqrt{34^2-4\cdot (-2) \cdot (-120)}}{2\cdot (-2)} = \\[2ex] & = \cfrac{-34\pm \sqrt{1156-960}}{-4} = \\[2ex] &= \cfrac{-34 \pm \sqrt{196}}{-4}= \\[1.5ex] & =\cfrac{-34 \pm 14}{-4} = \begin{cases} \cfrac{-34+14}{-4}= \cfrac{-20}{-4}=\bm{5} \\[3ex] \cfrac{-34-14}{-4}= \cfrac{-48}{-4}=\bm{12} \end{cases} \end{aligned}$

En este caso particular, las dos soluciones obtenidas con la ecuación de segundo grado ya son directamente la solución del problema, porque son las únicas opciones que cumplirán con las condiciones del problema. Así pues, los dos catetos del triángulo miden 5 cm y 12 cm.

Problema 19

Calcula las longitudes de los lados de un rectángulo cuyo perímetro mide 76 cm y su área es de 345 cm².

Ver solución

Aunque el planteamiento de este problema también se podría hacer con una única incógnita, en este caso lo resolveremos mediante un sistema de ecuaciones de segundo grado con dos incógnitas ya que así es más fácil.

En este caso llamaremos x a la base del rectángulo e y a su altura:

$x = \text{base del rect\'angulo}$

$y = \text{altura del rect\'angulo}$

Si el perímetro del rectángulo es de 76 cm, se debe cumplir la siguiente igualdad:

$2x+2y=76$

Por otro lado, el área del rectángulo es de 345 cm², por lo tanto:

$A= b\cdot h = x\cdot y = 345$

De este modo ya tenemos las dos ecuaciones que forman el sistema:

$\left.\begin{array}{l}2x+2y=76 \\[2ex] xy = 345 \end{array} \right\}$

Resolveremos el sistema de ecuaciones del problema con el método de sustitución. Así que despejamos la variable x de la primera ecuación:

$\left.\begin{array}{l}2x+2y=76 \\[2ex] xy = 345 \end{array} \right\} \begin{array}{l}\longrightarrow \ 2x=76-2y \ \longrightarrow \ x=38-y \\[2ex] & \end{array}$

Sustituimos la expresión obtenida en la otra ecuación:

$xy=345 \ \xrightarrow{x \ = \ 38-y} \ (38-y)y=345$

$38y-y^2=345$

$-y^2+38y-345=0$

Y resolvemos la ecuación cuadrática del problema aplicando la fórmula general:

$\begin{aligned} y&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-38\pm \sqrt{38^2-4\cdot (-1) \cdot (-345)}}{2\cdot (-1)} = \\[2ex] & = \cfrac{-38\pm \sqrt{1444-1380}}{-2} = \\[2ex] &= \cfrac{-38 \pm \sqrt{64}}{-2}= \\[1.5ex] & =\cfrac{-38 \pm 8}{-2} = \begin{cases} \cfrac{-38 + 8}{-2}=\cfrac{-30}{-2}= 15 \\[3ex] \cfrac{-38-8}{-2}=\cfrac{-46}{-2}= 23 \end{cases} \end{aligned}$

De modo que el valor de la incógnita x depende del valor de y:

$x=38-y \ \xrightarrow{y \ = \ 15} \ x =38-15=23$

$x=38-y \ \xrightarrow{y \ = \ 23} \ x =38-23=15$

Por lo tanto, el rectángulo del problema tiene como base 23 cm y como altura 15 cm, o viceversa, su base mide 15 cm y su altura 23 cm. Ambas soluciones son posibles ya que el enunciado no especifica qué lado es más grande.

Problema 20

Calcula los dos números impares positivos que son consecutivos y cuya suma de cuadrados es igual a 802.

Ver solución

Para forzar que un número sea impar, este se debe expresar algebraicamente de la siguiente manera:

$\text{n\'umero impar peque\~no}=2x+1$

Por lo tanto, el siguiente número impar será:

$\text{n\'umero impar siguiente}=2x+3$

Según el enunciado del problema, la suma de los cuadrados de los dos números da como resultado 802, por tanto:

$(2x+1)^2+(2x+3)^2 = 802$

Calculamos las 2 identidades notables con la fórmula del cuadrado de una suma:

$(2x)^2+2\cdot 2x\cdot 1+1^2+(2x)^2+2\cdot 2x\cdot 3+3^2 = 802$

$4x^2+4x+1+4x^2+12x+9= 802$

$8x^2+16x+10= 802$

$8x^2+16x+10- 802=0$

$8x^2+16x-792=0$

Y, por último, resolvemos la ecuación de segundo grado del problema:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-16\pm \sqrt{16^2-4\cdot 8 \cdot (-792)}}{2\cdot 8} = \\[2ex] & = \cfrac{-16\pm \sqrt{256+25344}}{16} = \\[2ex] &= \cfrac{-16 \pm \sqrt{25600}}{16}= \\[1.5ex] & =\cfrac{-16 \pm 160}{16} = \begin{cases} \cfrac{-16+160}{16}= \cfrac{144}{16}=9 \\[3ex] \cfrac{-16-160}{16}= \cfrac{-176}{16}=-11 \end{cases} \end{aligned}$

En este problema, el enunciado solo admite números positivos. Por lo que los dos números que satisfacen el enunciado son:

$\text{n\'umero impar peque\~no}=2x+1 = 2\cdot 9+1=\bm{19}$

$\text{n\'umero impar siguiente}=2x+3= 2\cdot 9+3 = \bm{21}$