En este post te explicamos qué es el método gráfico y cómo se resuelve un sistema de ecuaciones por el método gráfico. Además, podrás ver la explicación del método gráfico mediante un ejemplo resuelto por pasos y, finalmente, podrás practicar con varios ejercicios de sistemas de ecuaciones resueltos paso a paso por el método gráfico.
Índice
¿Qué es el método gráfico?
El método de gráfico es un método utilizado para resolver sistemas de ecuaciones. Concretamente, el método gráfico consiste en representar las ecuaciones del sistema en una gráfica y ver en qué punto se cortan (en el siguiente apartado veremos exactamente cómo se hace).
Existen más métodos para resolver sistemas de ecuaciones, como por ejemplo el método de sustitución, el método de reducción, o método de igualación. Si estás más interesad@ en estos otros métodos, puedes buscar la explicación de cada uno de ellos en esta web.
Cómo resolver un sistema de ecuaciones por el método gráfico
Para resolver un sistema de ecuaciones por el método gráfico se deben hacer los siguientes pasos:
- Despejar la incógnita y de las dos ecuaciones del sistema.
- Construir una tabla de valores para cada ecuación.
- Representar gráficamente las dos ecuaciones en el plano cartesiano. Se obtendrán dos rectas:
- Si las dos rectas se cortan en un punto, dicho punto de corte es la solución del sistema de ecuaciones (Sistema Compatible Determinado).
- Si las dos rectas se superponen, el sistema de ecuaciones tiene infinitas soluciones (Sistema Compatible Indeterminado).
- Si las dos rectas son paralelas (no se cortan), el sistema de ecuaciones no tiene solución (Sistema Incompatible).
El método gráfico es difícil de entender, por eso a continuación hemos resuelto paso a paso un sistema de ecuaciones lineales por el método gráfico para que veas cómo se aplica este procedimiento.
Ejemplo de un sistema de ecuaciones resuelto por el método gráfico
Vista la teoría sobre el método gráfico, vamos a explicar paso a paso la resolución de un sistema de ecuaciones utilizando el método gráfico a modo de ejemplo:
En primer lugar, tenemos que despejar la incógnita y de las dos ecuaciones que forman el sistema:
Una vez tenemos despejada la y de ambas ecuaciones, debemos hacer una tabla de valores para cada ecuación. Y para construir una tabla de valores simplemente tenemos que otorgar valores (los que quieras) a la incógnita x, hacer los cálculos que se indican en cada ecuación, y el valor obtenido será la coordenada y correspondiente a ese punto.
Entonces, creamos la tabla de valores para la primera ecuación:
Una vez hemos calculado la tabla de valores de una ecuación, debemos representar los puntos obtenidos en un gráfico. Recuerda que la primera coordenada de un punto, la coordenada x, corresponde al eje horizontal, y la segunda coordenada de un punto, la coordenada y, corresponde al eje vertical.
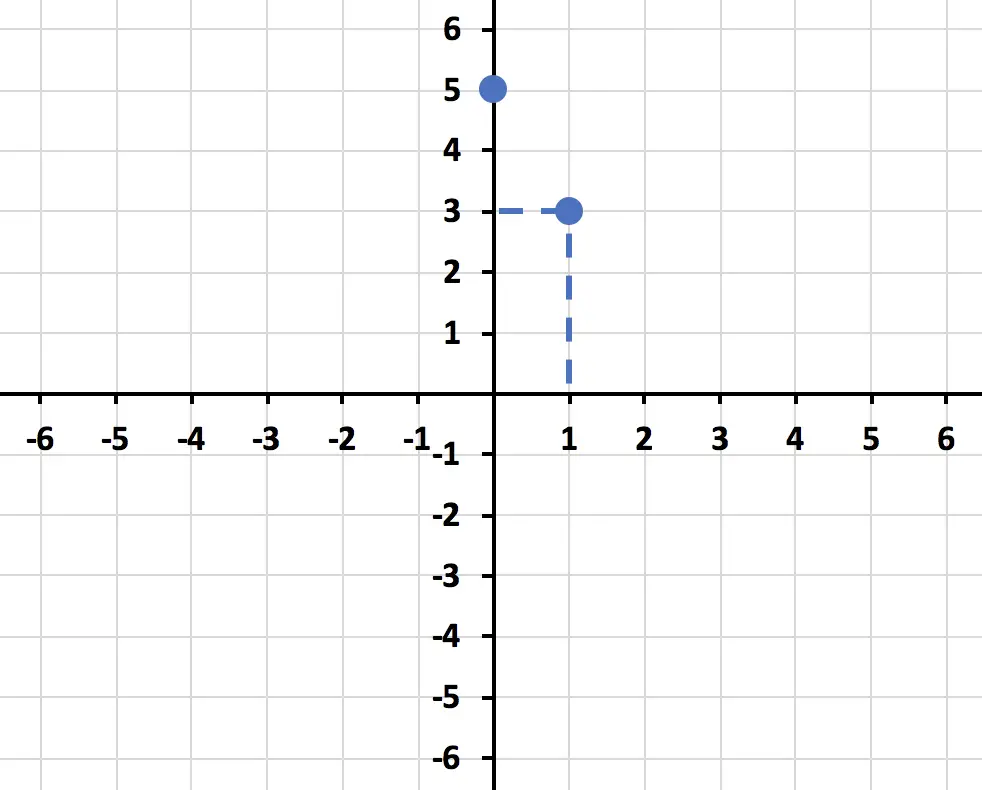
Y unimos los puntos representados para formar una recta:
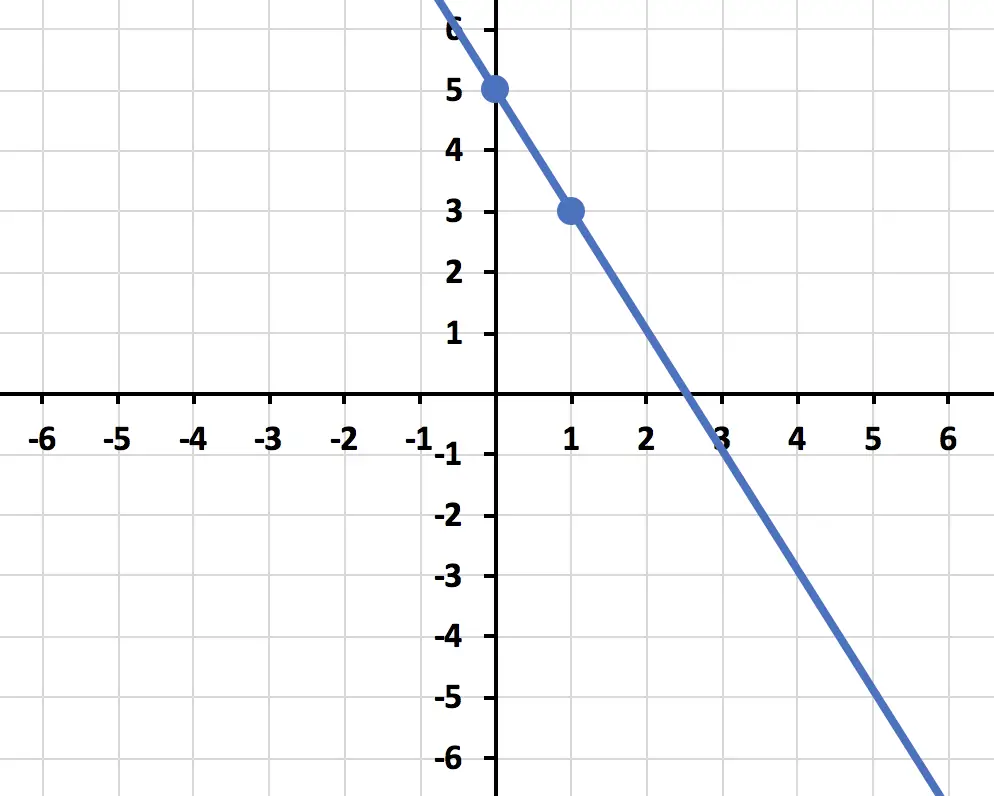
Aunque calculando dos puntos por cada ecuación es suficiente, si quieres puedes calcular algún otro punto para comprobar que la recta está bien representada.
Ahora debemos repetir el mismo proceso con la otra ecuación del sistema. Así pues, construimos la tabla de valores de la segunda ecuación:
Cuando ya tenemos la tabla de valores, representamos los puntos obtenidos en el mismo gráfico que hemos representado la recta anterior:
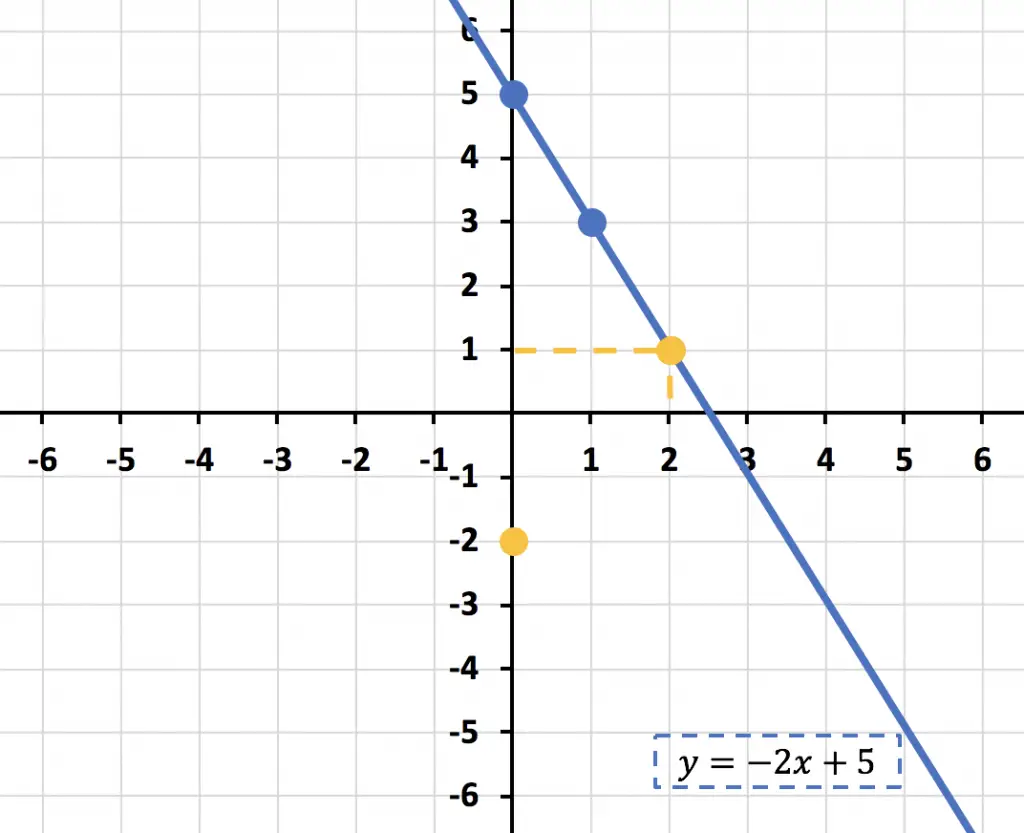
Y unimos los puntos para formar la otra recta:
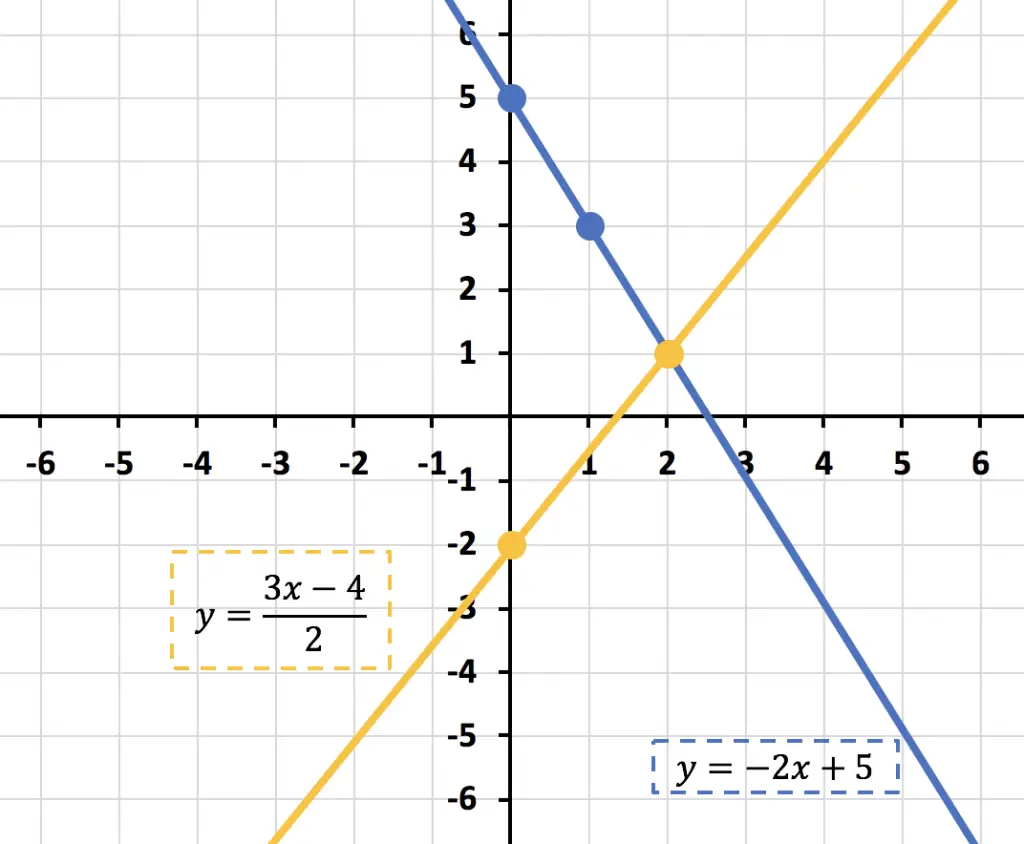
Una vez hemos representado las dos ecuaciones en un gráfico, ya podemos saber cuál es la solución del sistema de ecuaciones. La solución del sistema de ecuaciones es el punto donde se cortan las dos rectas, que en este caso es el punto (2,1):
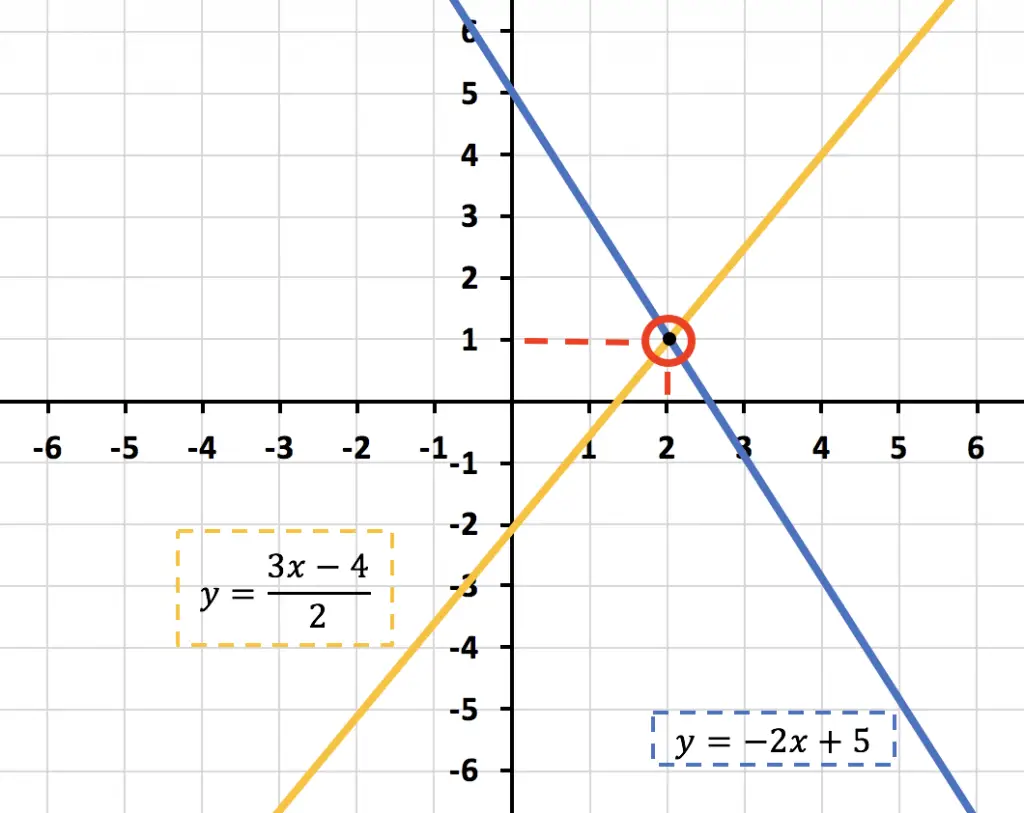
Como las rectas solamente se cruzan en el punto (2,1) la única solución del sistema de ecuaciones es:
En este caso, el sistema tiene una sola solución, por lo que se trata de un Sistema Compatible Determinado (SCD). Sin embargo, ten en cuenta que si las dos rectas estuvieran representadas una encima de la otra, el sistema tendría infinitas soluciones y por tanto sería un Sistema Compatible Indeterminado (SCI). Por otro lado, si las dos rectas fueran paralelas, el sistema no tendría ninguna solución y por tanto sería un Sistema Incompatible (SI).
Ejercicios resueltos por el método gráfico
Ejercicio 1
A continuación tienes representados gráficamente tres sistemas de ecuaciones diferentes. Determina qué tipo de sistema de ecuaciones es cada uno y cuál es su solución:
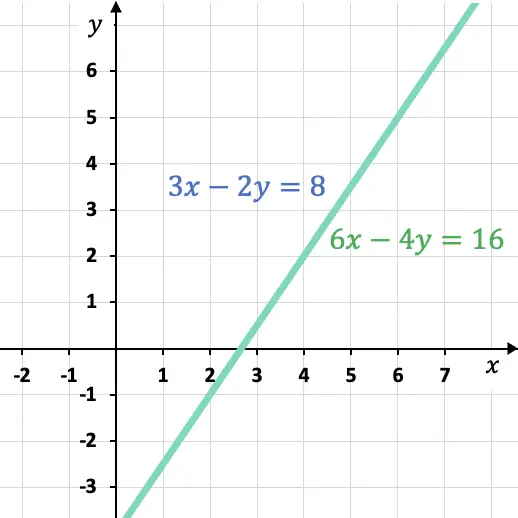
Las dos rectas representadas en el primer gráfico son coincidentes, es decir, están superpuestas. Lo que significa que se trata de un Sistema Compatible Indeterminado (SCI) y tiene infinitas soluciones.
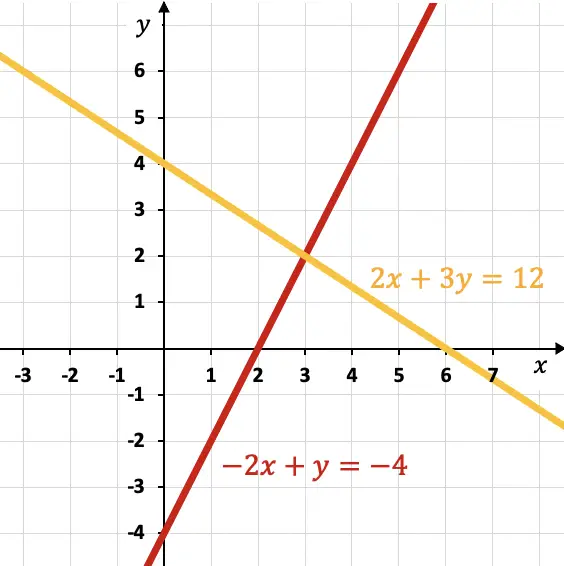
Las dos rectas rectas representadas en el segundo gráfico son secantes, por lo que tienen un único punto de corte. En consecuencia, es un Sistema Compatible Determinado (SCD) y tiene una única solución: x=3 ; y=2.
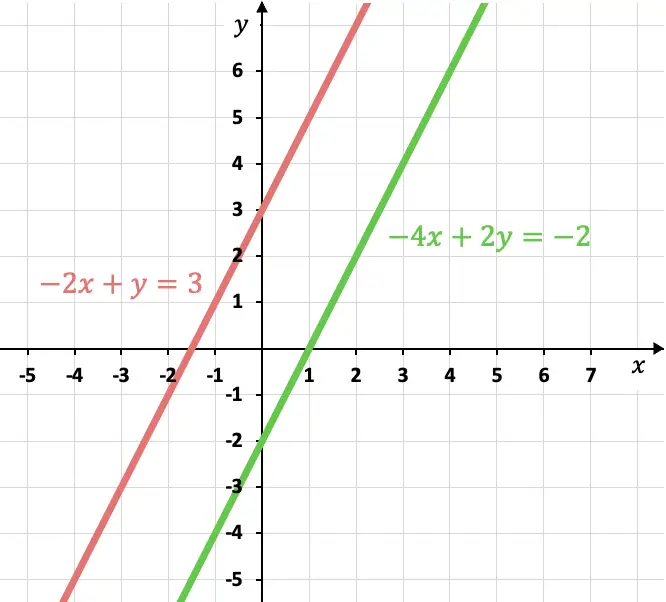
Las dos rectas rectas representadas en el último gráfico no se cortan nunca, con lo que son rectas paralelas. De modo que el sistema no tiene ninguna solución y, por tanto, es un Sistema Incompatible (SI).
Ejercicio 2
Resuelve el siguiente sistema de ecuaciones por el método gráfico:
Primero de todo, despejamos las incógnitas y de ambas ecuaciones del sistema:
Una vez tenemos despejada la y de las dos ecuaciones, debemos hacer una tabla de valores para cada ecuación. Así que construimos la tabla de valores de la primera ecuación:
Volvemos a hacer el mismo paso para la otra ecuación:
Y, finalmente, representamos gráficamente los puntos de las dos tablas de valores:
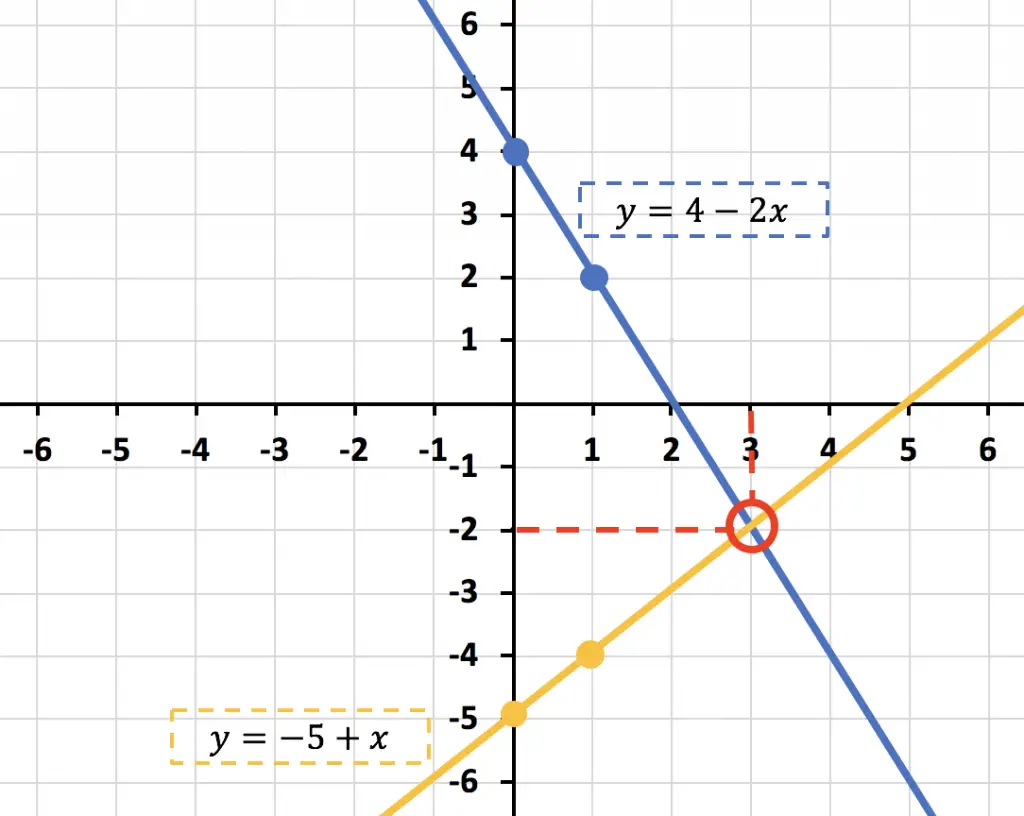
Las rectas se cruzan en el punto (3,-2). Por tanto, corresponde a un sistema de ecuaciones compatible determinado y su solución es:
Ejercicio 3
Resuelve el siguiente sistema de ecuaciones con fracciones por el método gráfico:
Lo primero que debemos hacer es despejar las incógnitas y de las dos ecuaciones que forman el sistema:
Ahora hacemos una tabla de valores con la primera ecuación:
Repetimos el procedimiento para la otra ecuación:
Y, por último, representamos gráficamente las dos ecuaciones:
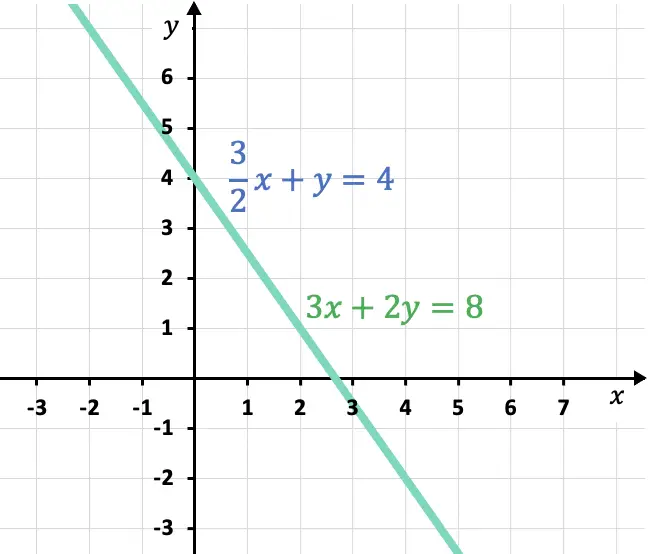
La representación gráfica de las dos ecuaciones corresponde a dos rectas coincidentes. Por lo que es un sistema compatible indeterminado (SCI) y el sistema tiene infinitas soluciones.
Ejercicio 4
Soluciona el siguiente sistema de ecuaciones por el método gráfico:
En primer lugar, despejamos las incógnitas y de todas las ecuaciones del sistema:
Luego, construimos una tabla de valores de la primera ecuación:
Hacemos la tabla de valores de la segunda ecuación:
Y representamos los puntos obtenidos en una gráfica para formar las dos rectas del sistema:
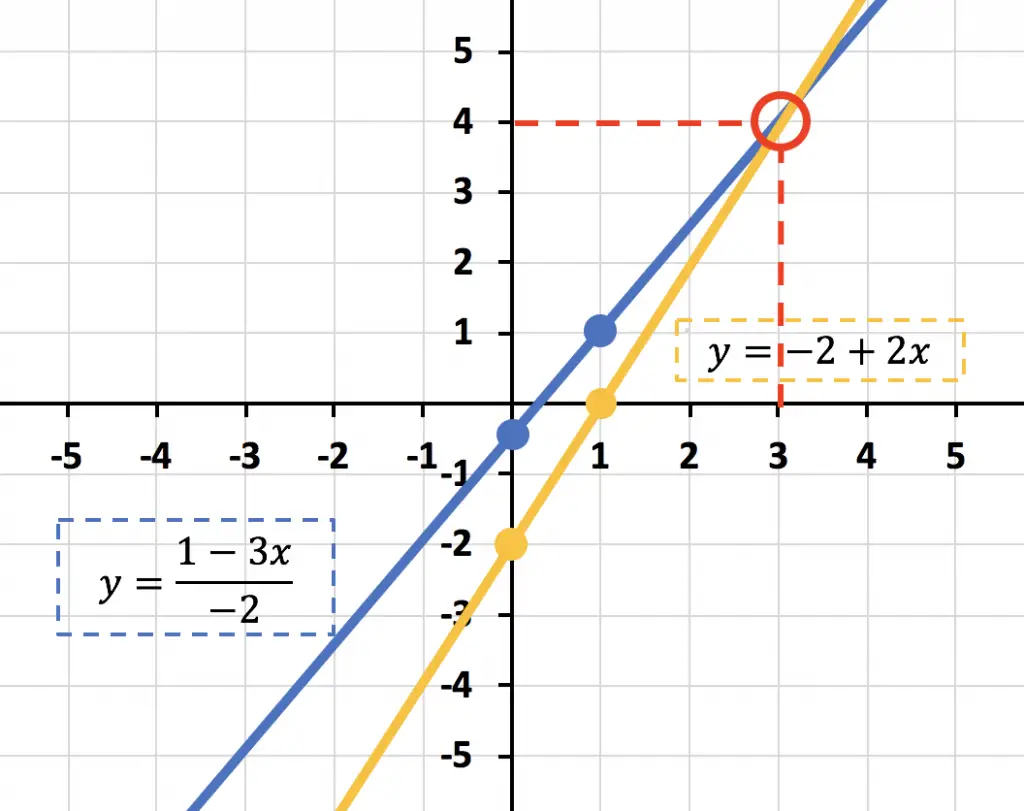
El punto de corte de las rectas es (3,4), así que la única solución del sistema de ecuaciones lineales es:
Ejercicio 5
Halla la solución del siguiente sistema de ecuaciones por el método gráfico:
El primer paso para aplicar el método gráfico es despejar las incógnitas y de las 2 ecuaciones:
Construimos una tabla de valores de la primera ecuación a partir de la expresión algebraica obtenida:
Hacemos la tabla de valores de la segunda ecuación a partir de su expresión matemática:
Y representamos las ecuaciones del sistema en un gráfico:
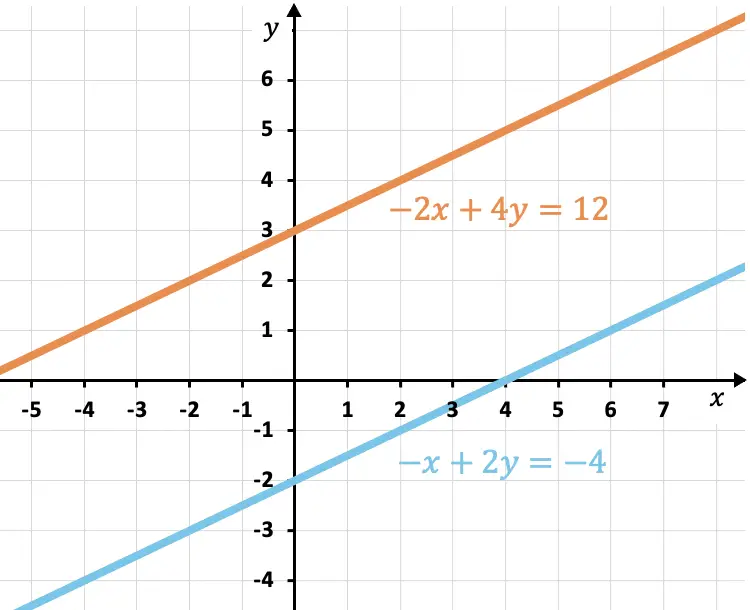
Sin embargo, las ecuaciones representadas nunca se cortan en la gráfica, es decir, se trata de dos rectas paralelas. Por lo tanto, es un Sistema Incompatible (SI) y es un sistema de ecuaciones sin solución.
Ejercicio 6
Calcula el siguiente sistema con dos ecuaciones y dos incógnitas por el método gráfico:
Primero de todo, tenemos que despejar las incógnitas y de ambas ecuaciones:
En segundo lugar, elaboramos la tabla de valores de la primera ecuación:
Luego calculamos la tabla de valores de la segunda ecuación:
Representamos los puntos calculados en el gráfico y los unimos para formar las rectas que representan las ecuaciones:
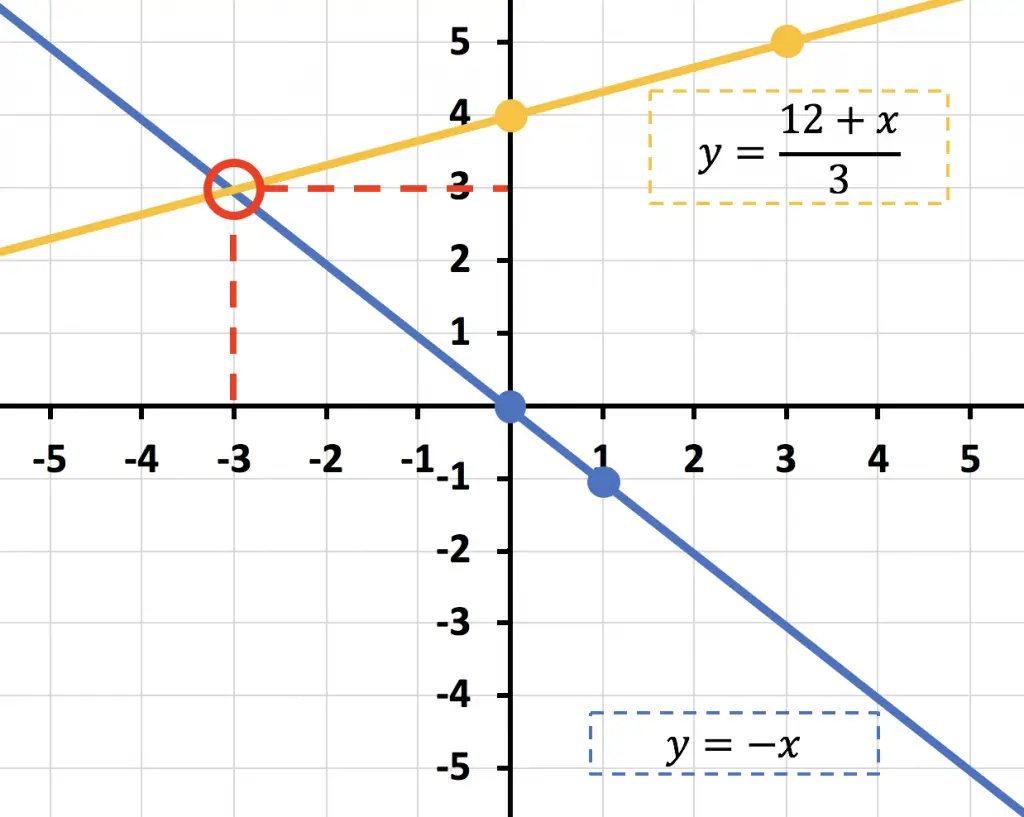
El punto de intersección de las rectas es (-3,3), por tanto, la única solución del sistema de ecuaciones es:
El procedimiento que hemos visto en este post es muy parecido al que se utiliza para resolver sistemas de inecuaciones con dos incógnitas. Puedes ver cómo se solucionan este tipo de sistemas en estos ejercicios resueltos de sistemas de inecuaciones con dos incógnitas.

Me ayudó demasiado gracias
¡Gracias a ti Leonel!
Gracias en verdad me ayudo a sistematizar el procedimiento el orden de los pasos.
¡Me alegro de que te resulte útil Ernesto!
excelente demostración me ayuda para mi trabajo del método gráfico
gracias
¡Genial Efrain! ¡Gracias por tu comentario!
La verdad estoy en 1er año y ya entiendo todo tipo de ecuaciones menos las diferenciales porque parece chino bueno gracias solo entre acá por los ejercicios
Siempre va bien repasar conceptos, ¡sigue así Isla!