▷ Problemas con ecuaciones de segundo grado

En esta página te explicamos cómo se resuelven los problemas con ecuaciones de segundo grado. También hemos resuelto 10 problemas con ecuaciones de segundo grado paso a paso para que puedas practicar. Además, puedes dejarnos tu problema en los comentarios que te lo resolveremos.

Índice

Cómo resolver problemas con ecuaciones de segundo grado

Para resolver un problema con una ecuación de segundo grado se deben seguir los siguientes pasos:

Identificar la incógnita del problema.
Plantear la ecuación de segundo grado del problema.
Resolver la ecuación de segundo grado.
Interpretar la solución obtenida.

El último paso se refiere a que debemos comprobar que la solución hallada de la ecuación realmente sea la solución del problema, ya que normalmente de las ecuaciones de segundo grado se obtienen dos soluciones, pero puede que alguna de ellas no pueda ser una solución factible del problema. Por ejemplo, si en un problema estamos buscando la edad de una persona, no tiene sentido que la solución del problema sea un número negativo.

Solucionamos tu problema de ecuaciones de segundo grado

Si tienes algún problema con una ecuación de segundo grado y no sabes cómo resolverlo, nos lo puedes dejar en los comentarios, que lo resolveremos rápidamente.

Problemas con ecuaciones de segundo grado resueltos

Lógicamente, antes de empezar a resolver problemas de ecuaciones cuadráticas debes tener claro los siguientes conceptos:

Así pues, para que puedas practicar, a continuación tienes la resolución de 10 ejercicios que corresponden a problemas con ecuaciones de segundo grado. Hemos resuelto todos los problemas paso a paso para que se entiendan lo mejor posible, pero si tienes alguna duda puedes preguntárnosla abajo en los comentarios.

Problema 1

La multiplicación de un número por su doble da 288. ¿Qué número es?

Ver solución

Lo primero que debemos hacer es identificar la incógnita del problema. En este caso, x es el número que queremos hallar:

$x = \text{n\'umero que buscamos}$

En segundo lugar, debemos plantear la ecuación de segundo grado del problema. Para ello, primero debemos expresar algebraicamente el doble del número:

$\text{doble del n\'umero que buscamos} = 2x$

El enunciado del problema nos dice que el número incógnita multiplicado por su doble es igual a 288, por tanto:

$x \cdot 2x =288$

Y, finalmente, resolvemos la ecuación de segundo grado incompleta del problema:

$2x^2 =288$

$x^2 = \cfrac{288}{2}$

$x^2 = 144$

$x = \pm \sqrt{144}$

$\bm{x = \pm 12}$

Por lo tanto, el número que buscamos puede ser dos opciones: 12 o -12. En este problema, la solución negativa también está bien, ya que en ningún caso el problema nos dice que el número debe ser positivo.

Problema 2

Marta tiene el triple de edad que Juan. Y si multiplicamos sus edades obtenemos el resultado de 48. ¿Qué edad tiene cada uno?

Ver solución

La incógnita del problema tiene que ser o la edad de Juan, o la edad de Marta. Aquí lo hemos resuelto con la edad de Juan, pero también se podría plantear el problema escogiendo la edad de Marta como incógnita.

$x = \text{edad de Juan}$

El enunciado del problema dice que Marta tiene el triple de edad que Juan. Por lo tanto, la edad de Marta corresponde a la siguiente expresión:

$3x = \text{edad de Marta}$

Entonces, el problema dice que el resultado de multiplicar las dos edades es igual a 48. Por lo tanto:

$\text{edad de Juan} \cdot \text{edad de Marta} = 48$

$x \cdot 3x = 48$

Una vez hemos encontrado la ecuación cuadrática del problema, la resolvemos:

$3x^2 = 48$

$x^2 = \cfrac{48}{3}$

$x^2 = 16$

$x= \pm \sqrt{16}$

$x= \pm 4$

Así pues, las dos posibles soluciones son +4 y -4. Pero, evidentemente, una edad no puede ser negativa, por lo que la única solución factible es +4.

De forma que las edades son:

$\text{edad de Juan} = x = \mathbf{4 \ a\~nos}$

$\text{edad de Marta} = 3x = 3 \cdot 4 = \mathbf{12 \ a\~nos}$

Problema 3

Hallar un número cuyo doble más su cuadrado da 195.

Ver solución

En este problema la única incógnita posible es el número que queremos calcular:

$x= \text{n\'umero que buscamos}$

Matemáticamente, el doble del número que buscamos y su cuadrado son:

$2x = \text{doble del n\'umero}$

$x^2 = \text{cuadrado del n\'umero}$

El enunciado explica que la suma del doble del número más su cuadrado es igual a 195, por lo tanto, la ecuación del problema es:

$2x+x^2=195$

Así que resolvemos la ecuación de segundo grado completa del problema aplicando la fórmula general:

$x^2+2x-195=0$

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-2\pm \sqrt{2^2-4\cdot 1 \cdot (-195)}}{2\cdot 1} = \\[2ex] & = \cfrac{-2\pm \sqrt{4+780}}{2} = \\[2ex] &= \cfrac{-2 \pm \sqrt{784}}{2}= \\[1.5ex] & =\cfrac{-2 \pm 28}{2} = \begin{cases} \cfrac{-2 + 28}{2}=\cfrac{26}{2}=\bm{13} \\[3ex] \cfrac{-2- 28}{2}=\cfrac{-30}{2}=\bm{-15} \end{cases} \end{aligned}$

En este problema, el enunciado no especifica el signo del número, de manera que puede ser tanto +13 como -15. De hecho, si sustituimos las dos soluciones en la ecuación cuadrática del problema, podemos comprobar que ambas soluciones cumplen con la ecuación.

Problema 4

La longitud de un campo de fútbol hace 30 metros más que de anchura. Y su área es de 7000 m². ¿Cuáles son las dimensiones del campo?

Ver solución

En primer lugar, identificamos la incógnita del problema. En este caso diremos que x es igual a los metros de ancho del campo, pero también se podría solucionar poniendo como incógnita la longitud del campo.

$x = \text{metros de ancho del campo}$

Así pues, el problema dice que la longitud del campo mide 30 metros más que su ancho, por tanto:

$x +30 = \text{metros de longitud del campo}$

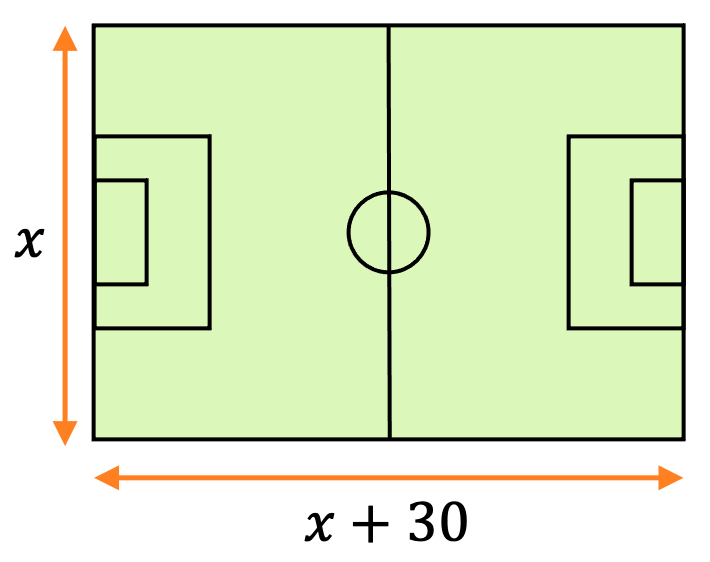
Problemas con ecuaciones de segundo grado con una incognita

Asimismo, el problema dice que el área del campo es 7000 m², por lo tanto, la ecuación cuadrática del problema es:

$A = b\cdot h$

$(x+30)\cdot x =7000$

$x^2+30x =7000$

Por último, resolvemos la ecuación cuadrática del problema:

$x^2+30x -7000=0$

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-30\pm \sqrt{30^2-4\cdot 1 \cdot (-7000)}}{2\cdot 1} = \\[2ex] & = \cfrac{-30\pm \sqrt{900+28000}}{2} = \\[2ex] &= \cfrac{-30 \pm \sqrt{28900}}{2}= \\[1.5ex] & =\cfrac{-30 \pm 170}{2} = \begin{cases} \cfrac{-30+170}{2}=\cfrac{140}{2} = 70 \\[3ex]\cfrac{-30-170}{2}=\cfrac{-200}{2} = -100 \end{cases} \end{aligned}$

En este problema, la interpretación de las soluciones obtenidas es importante, porque una dimensión de un campo no puede ser negativa. De modo que la única solución factible es x=70.

$\text{Ancho del campo} =x = \bm{70 \ m}$

$\text{Longitud del campo}=x+30=70+30=\bm{100 \ m}$

Problema 5

Al aumentar el lado de un cuadrado en 2 m, su área se cuadriplica. ¿Cuánto mide el lado original del cuadrado?

Ver solución

En este problema la incógnita será la longitud del lado del cuadrado original:

$x = \text{lado original del cuadrado}$

Como el área de un cuadrado se calcula multiplicando sus lados entre sí, el área original del cuadrado era:

$A=L\cdot L$

$x \cdot x = x^2 = \text{\'area del cuadrado original}$

El enunciado nos dice que si aumentamos 2 m la longitud del lado, su área se multiplica por 4. Por lo tanto, la ecuación de segundo grado del problema es:

$(x+2)\cdot (x+2)= 4\cdot x^2$

Ahora operamos los paréntesis aplicando la propiedad distributiva y agrupamos los términos semejantes:

$x^2+2x+2x+4= 4x^2$

$x^2+2x+2x+4-4x^2=0$

$-3x^2+4x+4=0$

Y solucionamos la ecuación cuadrática del problema utilizando la fórmula general:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{4\pm \sqrt{4^2-4\cdot (-3) \cdot 4}}{2\cdot (-3)} = \\[2ex] & = \cfrac{4\pm \sqrt{16+48}}{-6} = \\[2ex] &= \cfrac{4 \pm \sqrt{64}}{-6}= \\[1.5ex] & =\cfrac{4 \pm 16}{-6} = \begin{cases}\cfrac{4+16}{-6} =\cfrac{20}{-6} = -\cfrac{10}{3} \\[3ex]\cfrac{4-16}{-6} =\cfrac{-12}{-6} = 2\end{cases} \end{aligned}$

Lógicamente, la longitud inicial del cuadrado no podía ser negativa, por lo que la única solución posible es x=2.

$\text{Lado original del cuadrado} =x = \bm{2 \ m}$

Problema 6

Determina dos números positivos que se diferencian en 6 unidades y su producto es igual a 112.

Ver solución

Aunque el planteamiento de este problema se podría solucionar con dos incógnitas, para no tener que calcular un sistema de ecuaciones vamos a resolverlo mediante una ecuación de segundo grado con una sola incógnita.

En este caso llamaremos x al número más grande de los dos:

$x= \text{n\'umero grande}$

Como la diferencia entre los dos números es de 6 unidades, el otro número será:

$x-6= \text{n\'umero peque\~no}$

El producto de los dos números debe ser 112, por lo tanto:

$x\cdot (x-6)=112$

Eliminamos el paréntesis aplicando la propiedad distributiva:

$x^2-6x=112$

Y, por último, resolvemos la ecuación de segundo grado:

$x^2-6x-112=0$

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-(-6)\pm \sqrt{(-6)^2-4\cdot 1 \cdot (-112)}}{2\cdot 1} = \\[2ex] & = \cfrac{+6\pm \sqrt{36+448}}{2} = \\[2ex] &= \cfrac{6 \pm \sqrt{484}}{2}= \\[1.5ex] & =\cfrac{6 \pm 22}{2} = \begin{cases} \cfrac{6+22}{2}=\cfrac{28}{2}=14 \\[3ex] \cfrac{6-22}{2}=\cfrac{-16}{2}=-8 \end{cases} \end{aligned}$

En este problema, el enunciado solo admite números positivos. En consecuencia, la única solución factible del problema es:

$\text{n\'umero grande}=x=\bm{14}$

$\text{n\'umero peque\~no}=x-6=14-6=\bm{8}$

Problema 7

Si aumentamos la base de un cuadrado 25 cm y disminuimos su altura en 24 cm, obtenemos un rectángulo con la misma área. Calcula cuánto mide el lado del cuadrado.

Ver solución

La incógnita del problema se trata del dato que queremos calcular, esto es, el lado del cuadrado:

$x = \text{lado del cuadrado}$

De forma que los lados del rectángulo serán:

$\text{base rect\'angulo} = x+25$

$\text{altura rect\'angulo} = x-24$

Tanto el área de un cuadrado como la de un rectángulo se calculan con las siguientes fórmulas:

$A_{cuadrado}=L\cdot L = x \cdot x$

$A_{rect\'angulo}=b\cdot h =(x+25)\cdot (x-24)$

Por lo tanto, si ambas áreas deben ser iguales, se debe verificar la siguiente igualdad:

$A_{cuadrado}=A_{rect\'angulo}$

$x \cdot x=(x+25)\cdot (x-24)$

Hacemos las multiplicaciones:

$x^2=x^2-24x+25x-600$

Y resolvemos la ecuación de segundo grado del problema:

$x^2-x^2+24x-25x+600=0$

$-x+600=0$

En este problema las dos incógnitas elevadas al cuadrado se anulan, por lo que simplemente tenemos que despejar la x de la ecuación de primer grado resultante:

$600=x$

En definitiva, el lado del cuadrado mide 600 cm.

$\text{Lado del cuadrado} =x = \bm{600 \ cm}$

Problema 8

Determina cuánto miden los catetos de un triángulo rectángulo si juntos suman 17 cm y su hipotenusa mide 13 cm.

Ver solución

Para este problema llamaremos x a un cateto del triángulo

$x = \text{longitud de un cateto}$

De modo que si la longitud de los dos catetos suman 17 cm, el otro cateto debe medir:

$x+\text{longitud del otro cateto} = 17$

$\text{longitud del otro cateto} = 17-x$

problemas con ecuaciones de segundo grado para secundaria eso

Ahora podemos encontrar una ecuación que relaciona los tres lados del triángulo aplicando el teorema de Pitágoras:

$h^2=c^2+c^2$

$13^2=x^2+(17-x)^2$

Resolvemos la identidad notable con la fórmula de una resta al cuadrado:

$13^2=x^2+17^2-2\cdot 17\cdot x+x^2$

$169=x^2+289-34x+x^2$

Operamos:

$169-x^2-289+34x-x^2=0$

$-2x^2+34x-120=0$

Y, finalmente, resolvemos la ecuación de segundo grado del problema usando la fórmula general:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-34\pm \sqrt{34^2-4\cdot (-2) \cdot (-120)}}{2\cdot (-2)} = \\[2ex] & = \cfrac{-34\pm \sqrt{1156-960}}{-4} = \\[2ex] &= \cfrac{-34 \pm \sqrt{196}}{-4}= \\[1.5ex] & =\cfrac{-34 \pm 14}{-4} = \begin{cases} \cfrac{-34+14}{-4}= \cfrac{-20}{-4}=\bm{5} \\[3ex] \cfrac{-34-14}{-4}= \cfrac{-48}{-4}=\bm{12} \end{cases} \end{aligned}$

En este caso particular, las dos soluciones obtenidas con la ecuación de segundo grado ya son directamente la solución del problema, porque son las únicas opciones que cumplirán con las condiciones del problema. Así pues, los dos catetos del triángulo miden 5 cm y 12 cm.

Problema 9

Calcula las longitudes de los lados de un rectángulo cuyo perímetro mide 76 cm y su área es de 345 cm².

Ver solución

Aunque el planteamiento de este problema también se podría hacer con una única incógnita, en este caso lo resolveremos mediante un sistema de ecuaciones de segundo grado con dos incógnitas ya que así es más fácil.

En este caso llamaremos x a la base del rectángulo e y a su altura:

$x = \text{base del rect\'angulo}$

$y = \text{altura del rect\'angulo}$

Si el perímetro del rectángulo es de 76 cm, se debe cumplir la siguiente igualdad:

$2x+2y=76$

Por otro lado, el área del rectángulo es de 345 cm², por lo tanto:

$A= b\cdot h = x\cdot y = 345$

De este modo ya tenemos las dos ecuaciones que forman el sistema:

$\left.\begin{array}{l}2x+2y=76 \\[2ex] xy = 345 \end{array} \right\}$

Resolveremos el sistema de ecuaciones del problema con el método de sustitución. Así que despejamos la variable x de la primera ecuación:

$\left.\begin{array}{l}2x+2y=76 \\[2ex] xy = 345 \end{array} \right\} \begin{array}{l}\longrightarrow \ 2x=76-2y \ \longrightarrow \ x=38-y \\[2ex] & \end{array}$

Sustituimos la expresión obtenida en la otra ecuación:

$xy=345 \ \xrightarrow{x \ = \ 38-y} \ (38-y)y=345$

$38y-y^2=345$

$-y^2+38y-345=0$

Y resolvemos la ecuación cuadrática del problema aplicando la fórmula general:

$\begin{aligned} y&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-38\pm \sqrt{38^2-4\cdot (-1) \cdot (-345)}}{2\cdot (-1)} = \\[2ex] & = \cfrac{-38\pm \sqrt{1444-1380}}{-2} = \\[2ex] &= \cfrac{-38 \pm \sqrt{64}}{-2}= \\[1.5ex] & =\cfrac{-38 \pm 8}{-2} = \begin{cases} \cfrac{-38 + 8}{-2}=\cfrac{-30}{-2}= 15 \\[3ex] \cfrac{-38-8}{-2}=\cfrac{-46}{-2}= 23 \end{cases} \end{aligned}$

De modo que el valor de la incógnita x depende del valor de y:

$x=38-y \ \xrightarrow{y \ = \ 15} \ x =38-15=23$

$x=38-y \ \xrightarrow{y \ = \ 23} \ x =38-23=15$

Por lo tanto, el rectángulo del problema tiene como base 23 cm y como altura 15 cm, o viceversa, su base mide 15 cm y su altura 23 cm. Ambas soluciones son posibles ya que el enunciado no especifica qué lado es más grande.

Problema 10

Calcula los dos números impares positivos que son consecutivos y cuya suma de cuadrados es igual a 802.

Ver solución

Para forzar que un número sea impar, este se debe expresar algebraicamente de la siguiente manera:

$\text{n\'umero impar peque\~no}=2x+1$

Por lo tanto, el siguiente número impar será:

$\text{n\'umero impar siguiente}=2x+3$

Según el enunciado del problema, la suma de los cuadrados de los dos números da como resultado 802, por tanto:

$(2x+1)^2+(2x+3)^2 = 802$

Calculamos las 2 identidades notables con la fórmula del cuadrado de una suma:

$(2x)^2+2\cdot 2x\cdot 1+1^2+(2x)^2+2\cdot 2x\cdot 3+3^2 = 802$

$4x^2+4x+1+4x^2+12x+9= 802$

$8x^2+16x+10= 802$

$8x^2+16x+10- 802=0$

$8x^2+16x-792=0$

Y, por último, resolvemos la ecuación de segundo grado del problema:

$\begin{aligned} x&= \cfrac{-b\pm \sqrt{b^2-4ac}}{2a} = \\[2ex] & =\cfrac{-16\pm \sqrt{16^2-4\cdot 8 \cdot (-792)}}{2\cdot 8} = \\[2ex] & = \cfrac{-16\pm \sqrt{256+25344}}{16} = \\[2ex] &= \cfrac{-16 \pm \sqrt{25600}}{16}= \\[1.5ex] & =\cfrac{-16 \pm 160}{16} = \begin{cases} \cfrac{-16+160}{16}= \cfrac{144}{16}=9 \\[3ex] \cfrac{-16-160}{16}= \cfrac{-176}{16}=-11 \end{cases} \end{aligned}$

En este problema, el enunciado solo admite números positivos. Por lo que los dos números que satisfacen el enunciado son:

$\text{n\'umero impar peque\~no}=2x+1 = 2\cdot 9+1=\bm{19}$

$\text{n\'umero impar siguiente}=2x+3= 2\cdot 9+3 = \bm{21}$

Solucionamos tu problema de ecuaciones de segundo grado

Si tienes un problema y no sabes cómo resolverlo, nos lo puedes escribir abajo en los comentarios, que lo resolveremos rápidamente.

2 comentarios en “Problemas con ecuaciones de segundo grado (o cuadráticas)”

Mar
29/05/2021 a las 15:51

El área de un cuadrado se duplica al aumentar uno de sus lados 7 metros, cuál es la expresión algebraica?

Responder
1. Ejercicios de Ecuaciones
  05/06/2021 a las 20:17
  
  Hola Mar,
  
  Rara resolver este problema llamaremos x al lado del cuadrado y A al área del cuadrado.
  Entonces, se cumplirá la siguiente ecuación:
  $2A=(x+7)^2$
  
  Por lo que despejando la incógnita A de la ecuación anterior obtenemos su expresión algebraica:
  $A=\cfrac{(x+7)^2}{2}$

Cómo resolver problemas con ecuaciones de segundo grado

Problemas con ecuaciones de segundo grado resueltos

Problema 1

Problema 2

Problema 3

Problema 4

Problema 5

Problema 6

Problema 7

Problema 8

Problema 9

Problema 10

2 comentarios en “Problemas con ecuaciones de segundo grado (o cuadráticas)”

Deja un comentario Cancelar respuesta